题目内容
如图，在坡度为1：3的山坡上种树，要求株距（相邻两树间的水平距离）是6米，则斜坡上相邻两树间的坡面距离是 米（结果保留根号）．
2.
【解析】
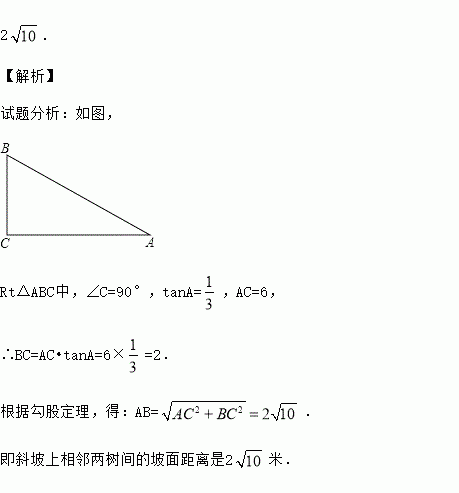
试题分析：如图，
Rt△ABC中，∠C=90°，tanA=，AC=6，
∴BC=AC•tanA=6×=2．
根据勾股定理，得：AB=．
即斜坡上相邻两树间的坡面距离是2米．
练习册系列答案
相关题目
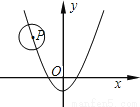
如图，已知⊙P的半径为2，圆心P在抛物线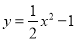
上运动，当⊙P与x轴相切时，圆心P的坐标为_____________
（，2）或（，2）
【解析】试题分析：依题意，可设P（x，2）或P（x，﹣2）．
①当P的坐标是（x，2）时，将其代入y=x2﹣1，得
2=x2﹣1，
解得x=±，
此时P（，2）或（﹣，2）；
②当P的坐标是（x，﹣2）时，将其代入y=x2﹣1，得
﹣2=x2﹣1，即﹣1=x2
无解．
综上所述，符合条件的点P的坐标是（，2）或（﹣，2） 二次函数y＝x2＋bx＋c的图象经过点(4，3)，(3，0)．
(1)求b、c的值；
(2)求出该二次函数图象的顶点坐标和对称轴；
(3)画出二次函数y＝x2＋bx＋c的图象．
(1)b＝－4，c＝3；(2) (2，－1)，x＝2；(3)画图见解析.
【解析】试题分析：（1）把已知点的坐标代入解析式，然后解关于b、c的二元一次方程组即可得解；
（2）把函数解析式转化为顶点式形式，然后即可写出顶点坐标与对称轴解析式；
（3）采用列表、描点法画出图象即可．
试题解析：（1）∵二次函数y=x2+bx+c的图象经过点（4，3），（3，0），
∴
解得
... 已知二次函数y＝－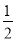
x2－7x＋
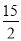，若自变量x分别取x1、x2、x3，且0＜x1＜x2＜x3，则对应的函数值y1、y2、y3的大小关系正确的是( )
A. y1＞y2＞y3 B. y1＜y2＜y3 C. y2＞y3＞y1 D. y2＜y3＜y1
A
【解析】∵二次函数y＝－x2－7x＋，∴此函数的对称轴为：x＝－＝－＝－7.∵0如图所示，一水库迎水坡AB的坡度i=1：2，求坡角α的正弦值sinα
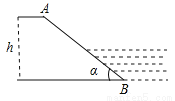
【解析】试题分析：首先过点A作AC⊥BC于点C，设AC=x，根据AC=x，根据坡比可得BC=2x，根据勾股定理求出AB的长度，然后根据正弦的求法得出答案．
试题解析：过A作AC⊥BC于C， ∵AB的坡度i=1：2，
∴tanα=， 设AC=x，BC=2x， 根据勾股定理可得：AB= ，
则sinα=． 如图，市政府准备修建一座高AB=6m的过街天桥，已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为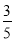
，则坡面AC的长度为（ ）m．
A．10 B．8 C．6 D．6
A.
【解析】
试题解析：∵天桥的坡面AC与地面BC的夹角∠ACB的正弦值为，
∴sinC=，
则，
解得：AC=10，
则坡面AC的长度为10m．
故选A． 如图，斜面AC的坡度（CD与AD的比）为1:2，AC=
米，坡顶有一旗杆BC，旗杆顶端B点与A点有一条彩带相连，若AB=10米，则旗杆BC的高度为（ ）
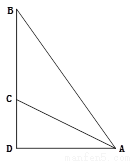
A. 5米 B. 6米 C. 8米 D.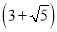 
米
A
【解析】试题分析：根据CD：AD=1:2，AC=3米可得：CD=3米，AD=6米，根据AB=10米，∠D=90°可得：BD==8米，则BC=BD－CD=8－3=5米. 当路程S一定时，速度υ与时间t之间的函数关系是 ( )
A. 正比例函数 B. 反比例函数 C. 一次函数 D. 二次函数
B
【解析】根据题意可知v=，由路程S一定，可知速度v与时间t之间的函数关系是反比例函数.
故选：B. 下列各式从左到右的变形中，是分解因式的是 ( )
A. x2-9+6x＝(x+3)(x-3)+6x B. (x+5)(x-2)＝x2+3x-10
C. x2-8x+16＝(x-4)2 D. (x-2)(x+3)＝(x+3)(x-2)
C
【解析】把一个多项式化成几个整式的积的形式，叫做把这个多项式分解因式.根据因式分解的定义可得，只有选项C符合因式分解的形式，故选C.