题目内容
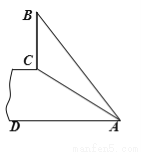
如图，斜坡AC的坡度（坡比）为1: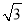 
，AC＝10米．坡顶有一垂直于水平面的旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，AB＝14米．试求旗杆BC的高度．
6米.
【解析】
试题分析：如果延长BC交AD于E点，则CE⊥AD，要求BC的高度，就要知道BE和CE的高度，就要先求出AE的长度．直角三角形ACE中有坡比，由AC的长，那么就可求出AE的长，然后求出BE、CE的高度，BC=BE-CE，即可得出结果．
试题解析：延长BC交AD于E点，则CE⊥AD．
在Rt△AEC中，AC=10，由坡比为1：可知：∠CAE=30°，
∴...
每年六七月份我市荔枝大量上市，今年某水果商以5元/千克的价格购进一批荔枝进行销售，运输过程中质量损耗5%，运输费用是0.7元/千克，假设不计其他费用．
（1）水果商要把荔枝售价至少定为多少才不会亏本？
（2）在销售过程中，水果商发现每天荔枝的销售量m（千克）与销售单价x（元/千克）之间满足关系：m= -10x+120，那么当销售单价定为多少时，每天获得的利润w最大？
（1）水果商要把荔枝售价至少定为6元/千克才不会亏本（2）当销售单价定为9元/千克时，每天可获利润w最大
【解析】分析：（1）设购进荔枝a千克，荔枝售价定为b元/千克时，水果商要不亏本，由题意建立不等式求出其值就可以了．
（2）由（1）可知，每千克荔枝的平均成本为6元，再根据售价-进价=利润就可以表示出w，然后化为顶点式就可以求出最值．
本题解析：
（1）设购进荔枝a千克，... 如图所示的是二次函数y＝ax2＋bx＋c的图象，则一次函数y=ax－b的图象不经过( )
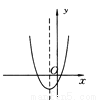
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
B
【解析】【解析】
由图象开口向上可知a＞0，对称轴x=＜0，得b＞0．所以一次函数y=y=ax﹣b的图象经过第一、三、四象限，不经过第二象限．故选B． 某厂今年一月份新产品的研发资金为a元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为____．
y＝a(1＋x)2
【解析】试题分析：∵一月份新产品的研发资金为a元，
2月份起，每月新产品的研发资金与上月相比增长率都是x，
∴2月份研发资金为，∴三月份的研发资金为．
故答案为： ． 已知二次函数y＝－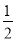
x2－7x＋
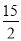，若自变量x分别取x1、x2、x3，且0＜x1＜x2＜x3，则对应的函数值y1、y2、y3的大小关系正确的是( )
A. y1＞y2＞y3 B. y1＜y2＜y3 C. y2＞y3＞y1 D. y2＜y3＜y1
A
【解析】∵二次函数y＝－x2－7x＋，∴此函数的对称轴为：x＝－＝－＝－7.∵0如图，当小杰沿坡度i=1：5的坡面由B到A行走了26米时，小杰实际上升高度AC=_________米．（可以用根号表示）
【解析】试题分析：根据坡度的定义可设AC=x，BC=5x，再根据勾股定理即可列方程求解.
由题意设AC=x，BC=5x，则，解得，
则小杰实际上升高度米. 如图，市政府准备修建一座高AB=6m的过街天桥，已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为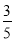
，则坡面AC的长度为（ ）m．
A．10 B．8 C．6 D．6
A.
【解析】
试题解析：∵天桥的坡面AC与地面BC的夹角∠ACB的正弦值为，
∴sinC=，
则，
解得：AC=10，
则坡面AC的长度为10m．
故选A． 如图，对称轴平行于y轴的抛物线与x轴交于(1，0)、(3，0)两点，则它的对称轴为____________________．
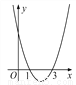
直线x＝2
【解析】试题分析：当两点到对称轴距离相等时，则所对应的函数值相等，则二次函数的对称轴为：x==2. (-2)2001+(-2)2002等于（ ）
A. -22001 B. -22002 C. 22001 D. -2
C
【解析】(-2)2001+(-2)2002=(-2)2001×(1-2)=22001，故选C.