题目内容
13.(1)解不等式$\frac{a+5}{2}$-1<$\frac{2a+1}{3}$.(2)解不等式组$\left\{\begin{array}{l}{\frac{x+5}{2}>x}\\{x-3(x-1)≤5}\end{array}\right.$并在数轴上表示出它的解集.
分析 (1)根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)去分母,得:3(a+5)-6<2(2a+1),
去括号,得:3a+15-6<4a+2,
移项,得:3a-4a<2-15+6,
合并同类项,得:-a<-7,
系数化为1,得:a>7;
(2)解不等式$\frac{x+5}{2}$>x,得:x<5,
解不等式x-3(x-1)≤5,得:x≥-1,
∴不等式组的解集为-1≤x<5,
将解集表示在数轴上如下:
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知?ABCD中,∠A+∠C=120°,则∠B的度数是( )
| A. | 120° | B. | 100° | C. | 80° | D. | 60° |
8.下列结论中,不正确的是( )
| A. | 如果两条直线都和第三条直线平行,那么这两条直线也互相平行 | |
| B. | 如果两条直线都和第三条直线垂直,那么这两条直线也互相垂直 | |
| C. | 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行 | |
| D. | 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行 |
18.若a,b,c为常数,且(a-c)2>a2+c2,则关于x的一元二次方程ax2+bx+c=0根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 有一个根或两个不相等的实数根 |
 如图,已知AC∥DE,∠A=∠E,BD=CF,求证:AB∥EF.
如图,已知AC∥DE,∠A=∠E,BD=CF,求证:AB∥EF.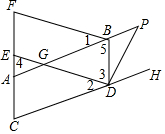 如图,已知点E,F为四边形ABDC的边CA的延长线上的两点,连接DE,BF,作∠BDH的平分线DP交AB的延长线于点P.若∠1=∠2,∠3=∠4,∠5=∠C.
如图,已知点E,F为四边形ABDC的边CA的延长线上的两点,连接DE,BF,作∠BDH的平分线DP交AB的延长线于点P.若∠1=∠2,∠3=∠4,∠5=∠C.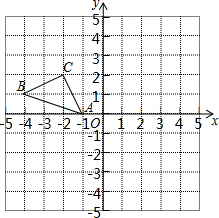 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题: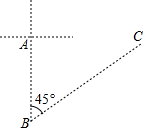 距沿海某城市A的正南方向300km的B处有一台风中心,根据海事预报,以台风中心为圆心,200km为半径的圆形区域内会受到台风影响.该台风中心现在正以18km\h的速度沿北偏东45°方向往C移动,问:该城市是否会受到这次台风的影响?请说明理由.($\sqrt{2}$≈1.4)
距沿海某城市A的正南方向300km的B处有一台风中心,根据海事预报,以台风中心为圆心,200km为半径的圆形区域内会受到台风影响.该台风中心现在正以18km\h的速度沿北偏东45°方向往C移动,问:该城市是否会受到这次台风的影响?请说明理由.($\sqrt{2}$≈1.4)