题目内容
12.已知$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$是方程组$\left\{\begin{array}{l}{2x+(m-1)y=2}\\{nx+y=1}\end{array}\right.$的解,则(m+n)2017的值为( )| A. | 22017 | B. | -1 | C. | 1 | D. | 0 |
分析 根据方程组的解满足方程组,可得关于m,n的方程组,根据解方程组,可得m,n的值,再根据1的任何次幂都等于1,可得答案.
解答 解:把$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{2x+(m-1)y=2}\\{nx+y=1}\end{array}\right.$,得
$\left\{\begin{array}{l}{2+m-1=2}\\{n+1=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=1}\\{n=0}\end{array}\right.$,
(m+n)2017=12017=1,
故选:C.
点评 本题考查了二元一次方程组的解,利用方程组的解满足方程组得出关于m,n的方程组是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2. 如图,AB∥EF∥CD,EG∥BD,且BD平分∠ABC,则图中与∠1相等的角(∠1除外)共有( )
如图,AB∥EF∥CD,EG∥BD,且BD平分∠ABC,则图中与∠1相等的角(∠1除外)共有( )
 如图,AB∥EF∥CD,EG∥BD,且BD平分∠ABC,则图中与∠1相等的角(∠1除外)共有( )
如图,AB∥EF∥CD,EG∥BD,且BD平分∠ABC,则图中与∠1相等的角(∠1除外)共有( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
1.已知?ABCD中,∠A+∠C=120°,则∠B的度数是( )
| A. | 120° | B. | 100° | C. | 80° | D. | 60° |
 如图,已知AC∥DE,∠A=∠E,BD=CF,求证:AB∥EF.
如图,已知AC∥DE,∠A=∠E,BD=CF,求证:AB∥EF.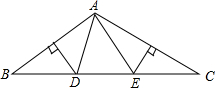 如图,在△ABC中,AB边垂直平分线交BC于点D,AC边垂直平分线交BC于点E,连接AD,AE.
如图,在△ABC中,AB边垂直平分线交BC于点D,AC边垂直平分线交BC于点E,连接AD,AE.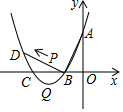 如图,已知抛物线y=x2+bx+c的顶点为Q,交y轴于点A(0,3),交x轴于B(-1,0),C两点,过点B作AB的垂线交抛物线于点D.
如图,已知抛物线y=x2+bx+c的顶点为Q,交y轴于点A(0,3),交x轴于B(-1,0),C两点,过点B作AB的垂线交抛物线于点D.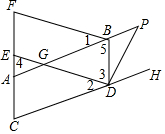 如图,已知点E,F为四边形ABDC的边CA的延长线上的两点,连接DE,BF,作∠BDH的平分线DP交AB的延长线于点P.若∠1=∠2,∠3=∠4,∠5=∠C.
如图,已知点E,F为四边形ABDC的边CA的延长线上的两点,连接DE,BF,作∠BDH的平分线DP交AB的延长线于点P.若∠1=∠2,∠3=∠4,∠5=∠C.