题目内容
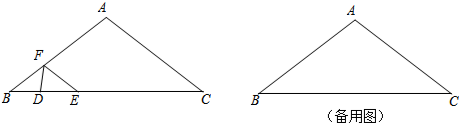
12．
如图，已知点P是线段AB的黄金分割点，且AP＞PB，设以AP为边长的正方形ACDP的面积为S1，以BF，AB的长为邻边的矩形AEFB的面积为S2，BF=PB，试问S1与S2有何关系？
分析 根据黄金分割的定义可得AP2=BP×AB，写出S1，S2的表达式，比较S1与S2的大小即可．
解答 解：∵点P是线段AB的黄金分割点，且AP＞BP，
∴AP2=BP×AB，
又∵S1=AP2，S2=BF×AB=PB×AB，
∴S1=S2．
点评 本题考查了黄金分割的知识，掌握黄金分割的表达式AP2=BP×AB是解题的关键．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“→“方向排列，如（1，0），（2，0），（2，1），（1，1），（1，2），（2，2）…根据这个规律，第82个点的坐标（10，0）．
7．下表中所列x，y的数值是某二次函数y=ax2+bx+c图象上的点所对应的坐标，其中x1＜x2＜x3＜x4＜x5＜x6＜x7，根据表中所提供的信息，以下判断正确的是（ ）①a＞0；②9＜m＜16；③k≤9；④b2≤4a（c-k）
| x | … | x1 | x2 | x3 | x4 | x5 | x6 | x7 | … |
| y | … | 16 | m | 9 | k | 9 | m | 16 | … |
| A． | ①② | B． | ③④ | C． | ①②④ | D． | ①③④ |