题目内容
7.下表中所列x,y的数值是某二次函数y=ax2+bx+c图象上的点所对应的坐标,其中x1<x2<x3<x4<x5<x6<x7,根据表中所提供的信息,以下判断正确的是( )①a>0;②9<m<16;③k≤9;④b2≤4a(c-k)| x | … | x1 | x2 | x3 | x4 | x5 | x6 | x7 | … |
| y | … | 16 | m | 9 | k | 9 | m | 16 | … |
| A. | ①② | B. | ③④ | C. | ①②④ | D. | ①③④ |
分析 首先根据x1<x2<x3<x4<x5<x6<x7,其对应的函数值是先减小后增加,可得抛物线开口向上,所以a>0;然后根据函数值是先减小后增加,可得k<9<m<16;最后根据a>0,可得二次函数有最小值,而且二次函数的最小值$\frac{4ac{-b}^{2}}{4a}≤k$,所以b2≥4a(c-k),据此判断即可.
解答 解:∵x1<x2<x3<x4<x5<x6<x7,其对应的函数值是先减小后增加,
∴抛物线开口向上,
∴a>0,①正确;
∴k<9<m<16,
∴9<m<16,②正确;
∴k<9,③不正确;
∵$\frac{4ac{-b}^{2}}{4a}≤k$,a>0,
∴4ac-b2≤4ak,
∴b2≥4a(c-k),④错误
综上,可得
判断正确的是:①②.
故选:A.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
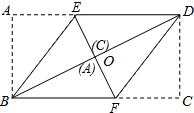 如图,将矩形纸片ABCD沿BE、DF折叠后,顶点A、C恰好都落在对角线BD的中点O处.若BD=6cm,则四边形BEDF的周长是8$\sqrt{3}$cm.
如图,将矩形纸片ABCD沿BE、DF折叠后,顶点A、C恰好都落在对角线BD的中点O处.若BD=6cm,则四边形BEDF的周长是8$\sqrt{3}$cm.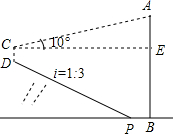 如图,斜坡下一块平地上有一直立的电线杆AB,小华从山坡下点P沿斜坡向上走15.8m到达点D,用高为1.5m的测角仪CD,测得电线杆顶端的仰角为10°,已知斜坡的坡度为i=1:3,山坡下点P到电线杆的距离PB为6m,求电线杆AB的高.(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,$\sqrt{10}$≈3.16,精确到0.1m)
如图,斜坡下一块平地上有一直立的电线杆AB,小华从山坡下点P沿斜坡向上走15.8m到达点D,用高为1.5m的测角仪CD,测得电线杆顶端的仰角为10°,已知斜坡的坡度为i=1:3,山坡下点P到电线杆的距离PB为6m,求电线杆AB的高.(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,$\sqrt{10}$≈3.16,精确到0.1m) 如图,已知点P是线段AB的黄金分割点,且AP>PB,设以AP为边长的正方形ACDP的面积为S1,以BF,AB的长为邻边的矩形AEFB的面积为S2,BF=PB,试问S1与S2有何关系?
如图,已知点P是线段AB的黄金分割点,且AP>PB,设以AP为边长的正方形ACDP的面积为S1,以BF,AB的长为邻边的矩形AEFB的面积为S2,BF=PB,试问S1与S2有何关系?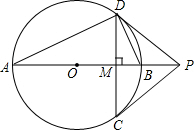 已知:如图,⊙O的直径AB垂直于弦CD于点M,过点C的切线与直径AB的延长线相交于点P,连结PD.
已知:如图,⊙O的直径AB垂直于弦CD于点M,过点C的切线与直径AB的延长线相交于点P,连结PD.