题目内容
12.观察下面计算过程:(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$) (1-$\frac{1}{3}$)(1+$\frac{1}{3}$)=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$=$\frac{1}{2}$×$\frac{4}{3}$;
(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$=$\frac{1}{2}$×$\frac{5}{4}$;
(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)(1-$\frac{1}{{5}^{2}}$)=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$×$\frac{4}{5}$×$\frac{6}{5}$=$\frac{1}{2}$×$\frac{6}{5}$;…
你发现了什么规律?用含n的式子表示这个规律,并用你发现的规律直接写出
(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{201{2}^{2}}$)的值.
分析 根据等式的变化找出变化规律“(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{{n}^{2}}$)=$\frac{1}{2}$×$\frac{n+1}{n}$(n≥2,且n为正整数)”,依据该规律即可解决问题.
解答 解:观察,发现规律:(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)=$\frac{1}{2}$×$\frac{4}{3}$,(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)=$\frac{1}{2}$×$\frac{5}{4}$,(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)(1-$\frac{1}{{5}^{2}}$)=$\frac{1}{2}$×$\frac{6}{5}$,…,
∴(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{{n}^{2}}$)=$\frac{1}{2}$×$\frac{n+1}{n}$(n≥2,且n为正整数).
当n=2012时,
(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{201{2}^{2}}$)=$\frac{1}{2}$×$\frac{2013}{2012}$=$\frac{2013}{4024}$.
点评 本题考查了规律型中的数字的变化类,解题的关键是找出规律“∴(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{{n}^{2}}$)=$\frac{1}{2}$×$\frac{n+1}{n}$(n≥2,且n为正整数)”.本题属于基础题,难度不大,解决该题型题目时,根据等式的变化找出变化规律是关键.

| 水平距离(米) | 8.50以上 | 8.49-8.00 | 7.99-7.50 | 7.49-7.00 | 69.00-6.50 | 6.49-6.00 | 5.99-5.60 | 5.59-5.20 | 5.19-4.80 | 4.79以下 |
| 得分 | 10分 | 9分 | 8分 | 7分 | 6分 | 5分 | 4分 | 3分 | 2分 | 1分 |
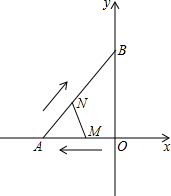 如图,在平面直角坐标系中,Rt△AOB的顶点A,B分别落在坐标轴上,O为原点,点A的坐标为(-12,0),点B坐标为(0,16),动点M从点O出发.沿OA向中点A以每秒2个单位的速度运动,同时动点N从A出发,沿AB向中点B以每秒$\frac{10}{3}$个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
如图,在平面直角坐标系中,Rt△AOB的顶点A,B分别落在坐标轴上,O为原点,点A的坐标为(-12,0),点B坐标为(0,16),动点M从点O出发.沿OA向中点A以每秒2个单位的速度运动,同时动点N从A出发,沿AB向中点B以每秒$\frac{10}{3}$个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).