题目内容
19. 如图,AB为半圆O的直径,直线CE与半圆O相切于点C,点D是$\widehat{AC}$的中点,CB=4,四边形ABCD的面积为2$\sqrt{2}$AC,则圆心O到直线CE的距离是4$\sqrt{2}$-2.
如图,AB为半圆O的直径,直线CE与半圆O相切于点C,点D是$\widehat{AC}$的中点,CB=4,四边形ABCD的面积为2$\sqrt{2}$AC,则圆心O到直线CE的距离是4$\sqrt{2}$-2.
分析 如图连接OD交AC于G,连接OC,根据S四边形ADCB=S△ADC+S△ABC,得到$\frac{1}{2}$•AC•DG+$\frac{1}{2}$•AC•BC=2$\sqrt{2}$AC,求出DG=2$\sqrt{2}$-4,OD=DG+OG=4$\sqrt{2}$-2,由此即可解决问题.
解答 解:如图连接OD交AC于G,连接OC.
∵$\widehat{AD}$=$\widehat{CD}$,
∴OD⊥AC,
∴AG=GC,∵OA=OB,
∴OG=$\frac{1}{2}$•BC=2,
∵S四边形ADCB=S△ADC+S△ABC,
∴$\frac{1}{2}$•AC•DG+$\frac{1}{2}$•AC•BC=2$\sqrt{2}$AC,
∴DG+4=4$\sqrt{2}$,
∴DG=2$\sqrt{2}$-4,
∴OD=DG+OG=4$\sqrt{2}$-2,
∵EC是切线,
∴OC⊥EC,
∴圆心O到直线CE的距离为4$\sqrt{2}$-2.
故答案为4$\sqrt{2}$-2.
点评 本题考查切线的性质、三角形的面积、三角形中位线定理等知识,解题的关键是学会用分割法求面积,属于中考常考题型.

练习册系列答案
相关题目
10.在下面四个立体图形中,从左面看与从正面看所得到的平面图形不相同的是( )
| A. |  正方体 | B. |  长方体 | C. |  球 | D. |  圆锥 |
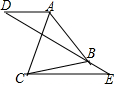 如图,直线DE过等边△ABC的顶点B,连接AD、CE,AD∥CE,∠E=30°,若BE:AD=1:$\sqrt{3}$,CE=4$\sqrt{3}$时,则BC=2$\sqrt{7}$.
如图,直线DE过等边△ABC的顶点B,连接AD、CE,AD∥CE,∠E=30°,若BE:AD=1:$\sqrt{3}$,CE=4$\sqrt{3}$时,则BC=2$\sqrt{7}$. 如图,已知直线BC、DE交于O点,OA、OF为射线,OA⊥BC,OF平分∠COE,∠COF=17°.
如图,已知直线BC、DE交于O点,OA、OF为射线,OA⊥BC,OF平分∠COE,∠COF=17°. 随着互联网的发展,同学们的学习习惯也有了改变,一些在做题遇到困难时,喜欢上网查找答案,针对这个问题,某校调查了部分学生对这种做法的意见(分为:赞成、无所谓、反对),并将调查结果绘制成图1和图2两个不完整的统计图,请根据图中提供的信息,解答下列问题:
随着互联网的发展,同学们的学习习惯也有了改变,一些在做题遇到困难时,喜欢上网查找答案,针对这个问题,某校调查了部分学生对这种做法的意见(分为:赞成、无所谓、反对),并将调查结果绘制成图1和图2两个不完整的统计图,请根据图中提供的信息,解答下列问题: