题目内容
9.已知:|m|=2,a、b互为相反数,且都不为0,c、d互为倒数,求2(a+b)+($\frac{a}{b}$-3cd)-m的值.分析 根据相反数、绝对值、倒数得出a+b=0,$\frac{a}{b}$=-1,cd=1,m=±2,再代入求出即可.
解答 解:∵|m|=2,a、b互为相反数,且都不为0,c、d互为倒数,
∴m=±2,a+b=0,$\frac{a}{b}$=-1,cd=1,
当m=2时,2(a+b)+($\frac{a}{b}$-3cd)-m=2×0+(-1-3×1)-2=-6,
当m=2时,2(a+b)+($\frac{a}{b}$-3cd)-m=2×0+(-1-3×1)-(-2)=-2.
点评 本题考查了相反数、绝对值、倒数和求代数式的值,能求出a+b=0、$\frac{a}{b}$=-1、cd=1、m=±2是解此题的关键

练习册系列答案
相关题目
9.下列语句准确规范的是( )
| A. | 直线a、b相交于点m | B. | 延长直线AB | ||
| C. | 延长射线AO到点B | D. | 直线AB、CD相交于点M |
20.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.已知线段MN=10cm,点C是直线MN上一点,NC=4cm,若P是线段MN的中点,Q是线段NC的中点,则线段PQ的长度是( )
| A. | 7cm | B. | 7cm或3cm | C. | 5cm | D. | 3cm |
14.已知(3a+b-4)2+|a+1|=0,则|3a-2b|的值为( )
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
18.下列说法正确的是( )
| A. | 长方形的长是a米,宽比长短25米,则它的周长可表示为(2a-25)米 | |
| B. | 6h表示底为6,高为h的三角形的面积 | |
| C. | 10a+b表示一个两位数,它的个位数字是a,十位数字是b | |
| D. | 甲、乙两人分别从相距40千米的两地相向出发,其行走的速度分别为3千米/小时和5千米/小时,经过x小时相遇,则可列方程为3x+5x=40 |
 已知△ABC中,AB=AC,∠ABC的平分线BD交AC于D点,若∠BDA=105°,求∠A的度数.
已知△ABC中,AB=AC,∠ABC的平分线BD交AC于D点,若∠BDA=105°,求∠A的度数.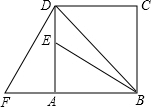 四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,∠F=60°,求:
四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,∠F=60°,求: 如图,AB为半圆O的直径,直线CE与半圆O相切于点C,点D是$\widehat{AC}$的中点,CB=4,四边形ABCD的面积为2$\sqrt{2}$AC,则圆心O到直线CE的距离是4$\sqrt{2}$-2.
如图,AB为半圆O的直径,直线CE与半圆O相切于点C,点D是$\widehat{AC}$的中点,CB=4,四边形ABCD的面积为2$\sqrt{2}$AC,则圆心O到直线CE的距离是4$\sqrt{2}$-2.