题目内容
14. 如图,已知直线BC、DE交于O点,OA、OF为射线,OA⊥BC,OF平分∠COE,∠COF=17°.
如图,已知直线BC、DE交于O点,OA、OF为射线,OA⊥BC,OF平分∠COE,∠COF=17°.求:∠AOD的度数.
分析 根据∠COF=17°,OF平分∠COE及∠COE是∠BOD的对顶角可得出∠BOD的度数,又根据OA⊥BC得出∠AOB=90°,最后结合图形算出∠AOD为124°.
解答 解:∵OF平分∠COE ,∠COF=17°,
,∠COF=17°,
∴∠COE=2∠COF=34°,
∵∠COE是∠BOD的对顶角,
∴∠BOD=∠COE=34°
∵OA⊥BC,
∴∠AOB=90,
∴∠AOD=∠AOB+∠BOD=34°+90°=124°,
答:∠AOD为124°.
点评 本题考查了垂线,角平分线的定义和对顶角,熟练掌握垂线,角平分线和对顶角的定义及角的计算方法是解题的关键.

练习册系列答案
相关题目
4.已知线段MN=10cm,点C是直线MN上一点,NC=4cm,若P是线段MN的中点,Q是线段NC的中点,则线段PQ的长度是( )
| A. | 7cm | B. | 7cm或3cm | C. | 5cm | D. | 3cm |
2.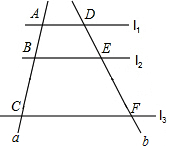 如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,则$\frac{DE}{DF}$等于( )
如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,则$\frac{DE}{DF}$等于( )
 如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,则$\frac{DE}{DF}$等于( )
如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,则$\frac{DE}{DF}$等于( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
9.下列等式从左到右的变形,属于因式分解的是( )
| A. | a(x-y)=ax-ay | B. | x2-9=(x+3)(x-3) | C. | (x+1)(x+2)=x2+3x+2 | D. | x2+2x+1=x(x+2)+1 |
6. 如图,△ABC≌△DCB,若AC=13,DE=4,则BE的长为( )
如图,△ABC≌△DCB,若AC=13,DE=4,则BE的长为( )
 如图,△ABC≌△DCB,若AC=13,DE=4,则BE的长为( )
如图,△ABC≌△DCB,若AC=13,DE=4,则BE的长为( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
3.已知-x2m-3+1=7是关于x的一元一次方程,则m的值是( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
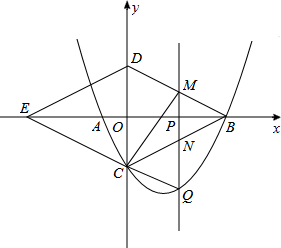 如图,抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$ x-4与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$ x-4与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q. 如图,AB为半圆O的直径,直线CE与半圆O相切于点C,点D是$\widehat{AC}$的中点,CB=4,四边形ABCD的面积为2$\sqrt{2}$AC,则圆心O到直线CE的距离是4$\sqrt{2}$-2.
如图,AB为半圆O的直径,直线CE与半圆O相切于点C,点D是$\widehat{AC}$的中点,CB=4,四边形ABCD的面积为2$\sqrt{2}$AC,则圆心O到直线CE的距离是4$\sqrt{2}$-2.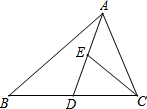 如图,在△ABC中,点D在BC边上,∠DAC=∠B.点E在AD边上,CD=CE.
如图,在△ABC中,点D在BC边上,∠DAC=∠B.点E在AD边上,CD=CE.