题目内容
16．
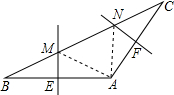在△ABC中，AB的垂直平分线交BC于M，交AB于E，AC的垂直平分线交BC于N，交AC于F．（1）若BC=7，求△AMN的周长；
（2）若∠BAC=130°，求∠MAN的度数．
分析 （1）根据线段垂直平分线的性质得到BM=AM，CN=AN，等量代换即可得到结论．
（2）首先由在△ABC中，∠BAC=130°，可求得∠C+∠B的度数，然后由AB、AC的垂直平分线分别交BC于点M、N，根据线段垂直平分线的性质，可得BM=AM，CN=AN，即可得∠CAN=∠C，∠BAM=∠B，继而求得∠CAN+∠BAM的度数，则可求得答案．
解答 解：（1）∵AB的垂直平分线交BC于M，交AB于E，AC的垂直平分线交BC于N，交AC于F，
∴BM=AM，CN=AN，
∴△AMN的周长=AM+MN+AN=BM+MN+CN=BC=7；
（2）∵∠BAC=130°，
∴∠B+∠C=50°，
由（1）证得BM=AM，CN=AN，
∴∠C=∠CAN，∠B=∠BAM，
∴∠CAN+∠BAM=∠C+∠B=50°，
∴∠MAN=130°-50°=80°．
点评 此题考查了线段垂直平分线的性质以及等腰三角形的性质．注意求得∠CAN+∠BAM=∠C+∠B是关键．
练习册系列答案
相关题目
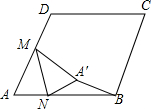如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′B，请求出A′B长度的最小值．
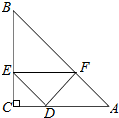如图，在等腰直角△ABC中，∠C=90°，AC=10，点D为AC边的一个动点（不与点A、C重合），过点D作DE∥AB，交BC于点E，再过点E作EF∥AC，交AB于点F．