题目内容
12.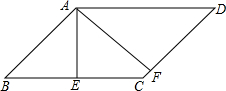 如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=2$\sqrt{2}$,则平行四边形ABCD的周长是( )
如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,∠EAF=45°,且AE+AF=2$\sqrt{2}$,则平行四边形ABCD的周长是( )| A. | 2 | B. | 4$\sqrt{2}$ | C. | 4 | D. | 8 |
分析 由AE⊥BC于E,AF⊥CD于F,∠EAF=45°,易求得∠C的度数,又由在平行四边形ABCD中,证得△ABE与△ADF是等腰直角三角形,继而求得答案.
解答 解:∵AE⊥BC,AF⊥CD,∠EAF=45°,
∴∠C=180°-90°-90°-45°=135°,
∵四边形ABCD是平行四边形,
∴∠B=∠D=180°-∠C=45°,
∴AB=$\sqrt{2}$AE,AD=$\sqrt{2}$AF,
∴AB+AD=$\sqrt{2}$(AE+AF)=$\sqrt{2}$×2$\sqrt{2}$=4,
∴平行四边形ABCD的周长是:4×2=8.
故选D.
点评 此题考查了平行四边形的性质以及等腰直角三角形性质.注意证得△ABE与△ADF是等腰直角三角形是关键.

练习册系列答案
相关题目
3.某中学为筹备校庆,准备印制一批纪念册,每册由4张彩页,6张黑白页构成.印制该纪念册的总费用由制版费和印刷费两部分组成,其中制版费的价格为:彩页300元/张,黑白页50元/张;印刷费用与印数的关系见表:
(1)印制这批纪念册需制版费1500元,印制1千册纪念册的印刷费13000元;
(2)若印制这批纪念册共需y元,则:
①当1≤x<5时,求y关于x的函数表达式;
②当y≤60 080元,最多能印多少册?
| 印数x(千册) | 1≤x<5 | x≥5 |
| 彩色(元/张) | 2.2 | 2.0 |
| 黑白(元/张) | 0.7 | 0.6 |
(2)若印制这批纪念册共需y元,则:
①当1≤x<5时,求y关于x的函数表达式;
②当y≤60 080元,最多能印多少册?
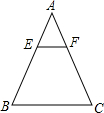 如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{3}$,S四边形BCFE=15,则S△ABC=16.
如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{3}$,S四边形BCFE=15,则S△ABC=16.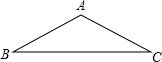 如图,在△ABC中,AB=AC=10,BC=10$\sqrt{3}$.
如图,在△ABC中,AB=AC=10,BC=10$\sqrt{3}$.
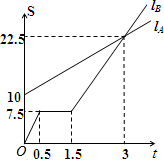 如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系.根据图象,回答下列问题:
如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系.根据图象,回答下列问题: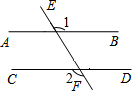 如图,直线AB,CD被EF所截,且AB∥CD,若∠1=126°,则∠2=126°.
如图,直线AB,CD被EF所截,且AB∥CD,若∠1=126°,则∠2=126°.