题目内容
20.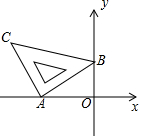 含45°角的直角三角板如图放置在平面直角坐标系中,其中A(-2,0),B(0,1),则直线BC的解析式为y=-$\frac{1}{3}$x+1.
含45°角的直角三角板如图放置在平面直角坐标系中,其中A(-2,0),B(0,1),则直线BC的解析式为y=-$\frac{1}{3}$x+1.
分析 过C作CD⊥x轴于点D,则可证得△AOB≌△CDA,可求得CD和OD的长,可求得C点坐标,利用待定系数法可求得直线BC的解析式.
解答 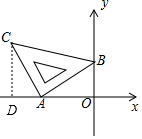 解:
解:
如图,过C作CD⊥x轴于点D,
∵∠CAB=90°,
∴∠DAC+∠BAO=∠BAO+∠ABO=90°,
∴∠DAC=∠ABO,
在△AOB和△CDA中
$\left\{\begin{array}{l}{∠ABO=∠CAD}\\{∠AOB=∠CDA}\\{AB=AC}\end{array}\right.$
∴△AOB≌△CDA(AAS),
∵A(-2,0),B(0,1),
∴AD=BO=1,CD=AO=2,
∴C(-3,2),
设直线BC解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-3k+b=2}\\{b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=1}\end{array}\right.$,
∴直线BC解析式为y=-$\frac{1}{3}$x+1,
故答案为:y=-$\frac{1}{3}$x+1.
点评 本题主要考查待定系数法及全等三角形的判定和性质,构造全等三角形求得C点坐标是解题的关键.

练习册系列答案
相关题目
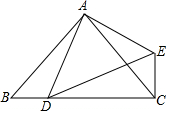 将两块大小不同的等腰直角三角板△ABC与△ADE(其中∠BAC=∠DAE=90°)按如图位置摆放,使点D恰好落在BC边上,求证:BD=CE.
将两块大小不同的等腰直角三角板△ABC与△ADE(其中∠BAC=∠DAE=90°)按如图位置摆放,使点D恰好落在BC边上,求证:BD=CE. 如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=6,DH=2,平移距离CF为3,则BE=3,阴影部分面积为15.
如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=6,DH=2,平移距离CF为3,则BE=3,阴影部分面积为15. 如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).