题目内容
8.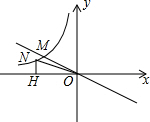 如图,正比例函数y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$交于M点,已知点M(-4,m),点N为此反比例函数图形上任意一点(不与点M重合),NH垂直于x轴于点H.
如图,正比例函数y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$交于M点,已知点M(-4,m),点N为此反比例函数图形上任意一点(不与点M重合),NH垂直于x轴于点H.(1)求反比例函数表达式;
(2)求△ONH的面积.
分析 (1)将M(-4,m)代入y=-$\frac{1}{2}$x,得到m=2,将M(-4,2)代入y=-$\frac{1}{2}$x,得到k=-8,即可得到结论;
(2)把N(a,b)代入y=-$\frac{8}{x}$,得到ab=-8,即可得到结论.
解答 解:(1)将M(-4,m)代入y=-$\frac{1}{2}$x,得m=2,
将M(-4,2)代入y=-$\frac{1}{2}$x,得k=-8,
所以反比例函数表达式为:y=-$\frac{8}{x}$;
(2)设N(a,b),由图知,a<0,b>0代入y=-$\frac{8}{x}$得ab=-8,
则S△ONH=$\frac{1}{2}$OH•HN=$\frac{1}{2}$(-a)•b=-$\frac{1}{2}$ab=4.
点评 本题考查了反比例函数与一次函数的交点问题,待定系数法确定m,k的值,三角形面积的计算,求得反比例函数表达式是解题的关键.

练习册系列答案
相关题目
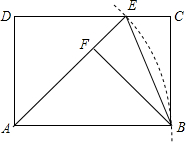 如图,在矩形ABCD中,以点A为圆心,AB长为半径画弧,交CD于点E,连接AE、BE.作BF⊥AE于点F.
如图,在矩形ABCD中,以点A为圆心,AB长为半径画弧,交CD于点E,连接AE、BE.作BF⊥AE于点F.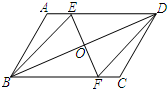 如图,在平行四边形ABCD中,BD的垂直平分线EF与AD交于点E,与BC交于点F,与BD交于点O.
如图,在平行四边形ABCD中,BD的垂直平分线EF与AD交于点E,与BC交于点F,与BD交于点O. 如图,一次函数y=kx-2的图象与反比例函数的图象交于A、B两点,过A作AC⊥x轴于点C,己知cos∠AOC=$\frac{2\sqrt{5}}{5}$,OA=$\sqrt{5}$
如图,一次函数y=kx-2的图象与反比例函数的图象交于A、B两点,过A作AC⊥x轴于点C,己知cos∠AOC=$\frac{2\sqrt{5}}{5}$,OA=$\sqrt{5}$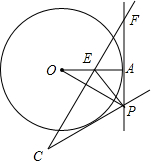 如图,P是⊙O的切线FA上的点,点A为切点,连接OP,OP的垂直平分线FE交OA于点E,连接EP,过点P作PC⊥EP
如图,P是⊙O的切线FA上的点,点A为切点,连接OP,OP的垂直平分线FE交OA于点E,连接EP,过点P作PC⊥EP 如图所示,某居民小区的A,B两楼之间的距离MN=30m,两楼高都是20m,A楼在B楼正南,B楼一楼朝南的窗台离地面的距离CN=2m,窗户高1.8m,正午时刻太阳光线与地面成30°角,A楼的影子是否影响B楼一楼窗户采光?若影响,挡住窗户多高?若不影响,请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)
如图所示,某居民小区的A,B两楼之间的距离MN=30m,两楼高都是20m,A楼在B楼正南,B楼一楼朝南的窗台离地面的距离CN=2m,窗户高1.8m,正午时刻太阳光线与地面成30°角,A楼的影子是否影响B楼一楼窗户采光?若影响,挡住窗户多高?若不影响,请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)