题目内容
19. 如图所示,某居民小区的A,B两楼之间的距离MN=30m,两楼高都是20m,A楼在B楼正南,B楼一楼朝南的窗台离地面的距离CN=2m,窗户高1.8m,正午时刻太阳光线与地面成30°角,A楼的影子是否影响B楼一楼窗户采光?若影响,挡住窗户多高?若不影响,请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)
如图所示,某居民小区的A,B两楼之间的距离MN=30m,两楼高都是20m,A楼在B楼正南,B楼一楼朝南的窗台离地面的距离CN=2m,窗户高1.8m,正午时刻太阳光线与地面成30°角,A楼的影子是否影响B楼一楼窗户采光?若影响,挡住窗户多高?若不影响,请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)
分析 设过E点的光线交地面于G点,如图,EM=FN=20m,MN=30m,CN=2m,CD=1.8m,利用含30度的直角三角形三边的关系,在Rt△EMG中计算出MG=20$\sqrt{3}$≈34.64>30,则可判断A楼的影子要落在B楼上,设PN为A楼在B楼上的影长,则在Rt△PNG中可计算出PN=$\frac{\sqrt{3}}{3}$NG=20-10$\sqrt{3}$≈2.68,然后计算PN-CN可判断A楼影子是否影响到B楼一楼采光.
解答 解:有影响.
设过E点的光线交地面于G点,如图,EM=FN=20m,MN=30m,CN=2m,CD=1.8m,
在Rt△EMG中,∵∠EGM=30°,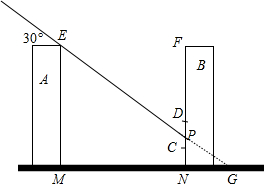
∴MG=$\sqrt{3}$EM=20$\sqrt{3}$≈34.64>30,
∴A楼的影子要落在B楼上,
设PN为A楼在B楼上的影长,
在Rt△PNG中,∵∠PGN=30°,NG=MG-MN=20$\sqrt{3}$-30,
∴PN=$\frac{\sqrt{3}}{3}$NG=20-10$\sqrt{3}$≈2.68,
∴PN-CN=2.68-2=0.68(m).
答:A楼影子影响到B楼一楼采光,挡住该户窗户0.68米.
点评 本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.熟练掌握含30度的直角三角形三边的关系是解决此题的关键.

练习册系列答案
相关题目
9. 如图所示,该几何体的主视图是( )
如图所示,该几何体的主视图是( )
 如图所示,该几何体的主视图是( )
如图所示,该几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
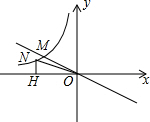 如图,正比例函数y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$交于M点,已知点M(-4,m),点N为此反比例函数图形上任意一点(不与点M重合),NH垂直于x轴于点H.
如图,正比例函数y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$交于M点,已知点M(-4,m),点N为此反比例函数图形上任意一点(不与点M重合),NH垂直于x轴于点H. 如图,某广场的形状是正方形,可以用64块地砖铺满,设计人员打算用黑、白两种颜色的地砖来铺,并且使上空的一只小鸽子随机地落在广场上时,落在黑色地砖上的概率是$\frac{11}{32}$,请你帮助设计人员设计一种铺设地砖的方案.(把铺褐色地砖的地方涂黑,使设计的图案美观,且是轴对称图形)
如图,某广场的形状是正方形,可以用64块地砖铺满,设计人员打算用黑、白两种颜色的地砖来铺,并且使上空的一只小鸽子随机地落在广场上时,落在黑色地砖上的概率是$\frac{11}{32}$,请你帮助设计人员设计一种铺设地砖的方案.(把铺褐色地砖的地方涂黑,使设计的图案美观,且是轴对称图形)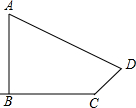 如图,学校旗杆附近有一斜坡,小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=12m,斜坡坡面上的影长CD=4m,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角.求旗杆AB的高度.(结果保留一位小数,参考数据:$\sqrt{3}$≈1.732).
如图,学校旗杆附近有一斜坡,小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=12m,斜坡坡面上的影长CD=4m,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角.求旗杆AB的高度.(结果保留一位小数,参考数据:$\sqrt{3}$≈1.732).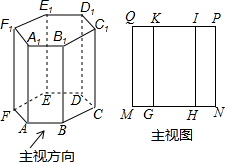 如图为一个几何体和它的主视图,请完成下面填空.
如图为一个几何体和它的主视图,请完成下面填空.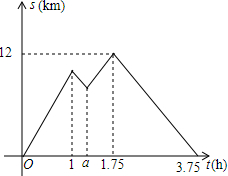 淆明小长假,李梅陋父母一起去青岛游玩.他们乘坐了一艘可远行12km的船在海上观光,该船远行时顺流匀速行驶.返回时则逆流匀速行驶.远行途中.李梅发现自己携带的游泳圈不知何时落入水中,于是该船立刻原路返回,一刻钟后找到游泳圈,随后继续远行,行驶到离出发地12km远的地方后没有停留又立刻返回.已知游泳圈的漂流速度和水流速度相同,船在远行和返回途中的静水速度相间.船与出发地的距离s(km)与行驶时间t(h)之间的函数图象如图所示.
淆明小长假,李梅陋父母一起去青岛游玩.他们乘坐了一艘可远行12km的船在海上观光,该船远行时顺流匀速行驶.返回时则逆流匀速行驶.远行途中.李梅发现自己携带的游泳圈不知何时落入水中,于是该船立刻原路返回,一刻钟后找到游泳圈,随后继续远行,行驶到离出发地12km远的地方后没有停留又立刻返回.已知游泳圈的漂流速度和水流速度相同,船在远行和返回途中的静水速度相间.船与出发地的距离s(km)与行驶时间t(h)之间的函数图象如图所示.