题目内容
17.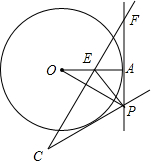 如图,P是⊙O的切线FA上的点,点A为切点,连接OP,OP的垂直平分线FE交OA于点E,连接EP,过点P作PC⊥EP
如图,P是⊙O的切线FA上的点,点A为切点,连接OP,OP的垂直平分线FE交OA于点E,连接EP,过点P作PC⊥EP(1)已知OA=8,AP=4,求OE的长
(2)求证:PC与⊙O相切.
分析 (1)由AP是⊙O的切线,得到∠OAP=90°,根据勾股定理列方程即可得到结论;
(2)过O作OG⊥PC于G,根据余角的性质得到∠OPE+∠OPC=90°=∠AOP+∠OPA,等量代换得到∠OPC=∠OPA,推出△AOP≌△GOP,根据全等三角形的性质得到OG=OA,即可得到结论.
解答 (1)解:∵AP是⊙O的切线,
∴∠OAP=90°,
∴PE2-AE2=AP2,
∵OA=8,AP=4,
∵OP的垂直平分线FE交OA于点E,
∴OE=PE,
∴OE2-(8-OE)2=42,
∴OE=5;
(2)证明:过O作OG⊥PC于G, ∵CE垂直平分OP,
∵CE垂直平分OP,
∴∠AOP=∠OPE,
∴∠OPE+∠OPC=90°=∠AOP+∠OPA,
∴∠OPC=∠OPA,
在△AOP与△POG中,
$\left\{\begin{array}{l}{∠OAP=∠OGP=90°}\\{∠OPG=∠OPA}\\{OP=OP}\end{array}\right.$,
∴△AOP≌△GOP(AAS),
∴OG=OA,
∴PC与⊙O相切.
点评 本题考查了切线的判定和性质.全等三角形的判定和性质,线段垂直平分线的性质,正确的作出辅助线构造全等三角形的是解题的关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
7.下列调查中,不适合采用全面调查方式的是( )
| A. | 了解全班同学每周进行体育锻炼的时间 | |
| B. | 对旅客上飞机前进行的安检 | |
| C. | 学校招聘教师,对应聘人员进行面试 | |
| D. | 了解全市中小学生每天的零花钱 |
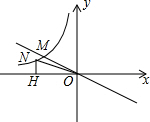 如图,正比例函数y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$交于M点,已知点M(-4,m),点N为此反比例函数图形上任意一点(不与点M重合),NH垂直于x轴于点H.
如图,正比例函数y=-$\frac{1}{2}$x与反比例函数y=$\frac{k}{x}$交于M点,已知点M(-4,m),点N为此反比例函数图形上任意一点(不与点M重合),NH垂直于x轴于点H. 如图,以AB为直径的⊙O交△ABC的边AC于D、BC于E,过D作⊙O的切线交BC于F,交BA延长线于G,且DF⊥BC.
如图,以AB为直径的⊙O交△ABC的边AC于D、BC于E,过D作⊙O的切线交BC于F,交BA延长线于G,且DF⊥BC.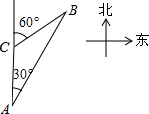 如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.此时轮船与灯塔的距离为( )
如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.此时轮船与灯塔的距离为( ) 如图,某广场的形状是正方形,可以用64块地砖铺满,设计人员打算用黑、白两种颜色的地砖来铺,并且使上空的一只小鸽子随机地落在广场上时,落在黑色地砖上的概率是$\frac{11}{32}$,请你帮助设计人员设计一种铺设地砖的方案.(把铺褐色地砖的地方涂黑,使设计的图案美观,且是轴对称图形)
如图,某广场的形状是正方形,可以用64块地砖铺满,设计人员打算用黑、白两种颜色的地砖来铺,并且使上空的一只小鸽子随机地落在广场上时,落在黑色地砖上的概率是$\frac{11}{32}$,请你帮助设计人员设计一种铺设地砖的方案.(把铺褐色地砖的地方涂黑,使设计的图案美观,且是轴对称图形)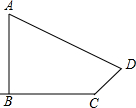 如图,学校旗杆附近有一斜坡,小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=12m,斜坡坡面上的影长CD=4m,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角.求旗杆AB的高度.(结果保留一位小数,参考数据:$\sqrt{3}$≈1.732).
如图,学校旗杆附近有一斜坡,小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=12m,斜坡坡面上的影长CD=4m,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角.求旗杆AB的高度.(结果保留一位小数,参考数据:$\sqrt{3}$≈1.732).