题目内容
20.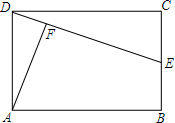 如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,证明△AFD∽△DCE,并计算点A至直线DE的距离(精确到0.1)
如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,证明△AFD∽△DCE,并计算点A至直线DE的距离(精确到0.1)
分析 由四边形ABCD 是矩形,得到∠ADC=∠C=90°,CD=AB=3,BC=AD=2,根据勾股定理得到DE=$\sqrt{C{D}^{2}+C{E}^{2}}$=$\sqrt{10}$,通过△ADF∽△DCE,得到$\frac{CD}{DE}=\frac{AF}{AD}$,列方程即可得到结果.
解答 解:∵四边形ABCD是矩形,
∴∠ADC=∠C=90°,CD=AB=3,BC=AD=2,
∴DE=$\sqrt{C{D}^{2}+C{E}^{2}}$=$\sqrt{10}$,
∵AF⊥DE,
∴∠AFD=∠C=90°,
∴∠DAF+∠ADF=∠ADF+∠CDE=90°,
∴∠DAF=∠CDE,∴△ADF∽△DCE
,∴$\frac{CD}{DE}=\frac{AF}{AD}$,即$\frac{3}{\sqrt{10}}=\frac{AF}{2}$,
∴AF=$\frac{3\sqrt{10}}{5}$≈1.9.
点评 本题考查了矩形的性质,相似三角形的判定和性质,勾股定理,证得△ADF∽△DCE是解题的关键.

练习册系列答案
相关题目
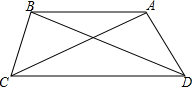 在四边形ABCD中,∠DAC=98°,∠DBC=82°,∠BCD=70°,BC=AD,则∠ACD=28°.
在四边形ABCD中,∠DAC=98°,∠DBC=82°,∠BCD=70°,BC=AD,则∠ACD=28°. 如图,正方形ABCD中,CD=5,BE=CF,且DG2+GE2=28,则AE的长$\sqrt{3}$.
如图,正方形ABCD中,CD=5,BE=CF,且DG2+GE2=28,则AE的长$\sqrt{3}$.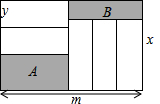 如图,长为m,宽为x(m>x)的大长方形被分割成7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为y,记阴影A与B的面积差为S.
如图,长为m,宽为x(m>x)的大长方形被分割成7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为y,记阴影A与B的面积差为S. 已知在△ABC中,∠B=60°,∠C=90°,CE、AD分别为∠C、∠A的角平分线,求证:EF=FD.
已知在△ABC中,∠B=60°,∠C=90°,CE、AD分别为∠C、∠A的角平分线,求证:EF=FD. 如图,在△ABC中,AB=6,AC=8,∠CAB=60°.求△ABC的内切圆⊙I的半径和外接圆⊙O的半径.
如图,在△ABC中,AB=6,AC=8,∠CAB=60°.求△ABC的内切圆⊙I的半径和外接圆⊙O的半径.