题目内容
10.解方程组:$\left\{\begin{array}{l}{|x-1|+|y-5|=1}\\{y=5+|x-1|}\end{array}\right.$.分析 方程组第二个等式变形得到③,根据绝对值的结果为非负数确定出y-5大于等于0,把③代入①求出y的值,进而求出x的值,即可确定出方程组的解.
解答 解:$\left\{\begin{array}{l}{|x-1|+|y-5|=1①}\\{y=5+|x-1|②}\end{array}\right.$,
由②得:y-5=|x-1|≥0③,
∴y-5≥0,
把③代入①得:y-5+|y-5|=1,即y-5+y-5=1,
解得:y=5.5,
把y=5.5代入②得:|x-1|=0.5,
解得:x1=1.5,x2=0.5,
则方程组的解为$\left\{\begin{array}{l}{x=1.5}\\{y=5.5}\end{array}\right.$,$\left\{\begin{array}{l}{x=0.5}\\{y=5.5}\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
2.下列计算正确的是( )
| A. | x2+x=2x2 | B. | (-a2)4=-a12 | C. | (3a3)2=9a6 | D. | x11÷x4•x2=x8 |
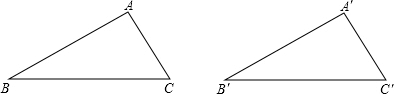
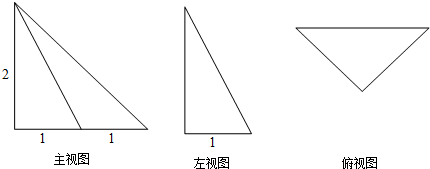
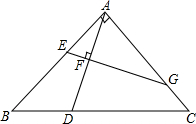 如图,等腰三角形ABC中,∠BAC=90°,AB=AC,点D在BC上,点F在AD上,过点F作EG⊥AD,交AB于E,AC于G,猜测AE,AG,BD,BC之间是否成比例,并说明理由.
如图,等腰三角形ABC中,∠BAC=90°,AB=AC,点D在BC上,点F在AD上,过点F作EG⊥AD,交AB于E,AC于G,猜测AE,AG,BD,BC之间是否成比例,并说明理由.
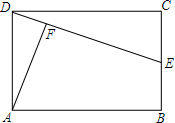 如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,证明△AFD∽△DCE,并计算点A至直线DE的距离(精确到0.1)
如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,证明△AFD∽△DCE,并计算点A至直线DE的距离(精确到0.1)