题目内容
11.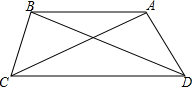 在四边形ABCD中,∠DAC=98°,∠DBC=82°,∠BCD=70°,BC=AD,则∠ACD=28°.
在四边形ABCD中,∠DAC=98°,∠DBC=82°,∠BCD=70°,BC=AD,则∠ACD=28°.
分析 以CD为对称轴作△CDE与△CBD对称,可得∠DEC=∠DBC=82°,CE=CB,然后由∠DAC=98°可得∠DEC+∠DAC=180°,得出A、D、E、C四点共圆,然后可得CE=AD,继而得出∠DCA=∠CDE=∠CDB,由∠BCD和∠DBC的度数可求出∠BCD的度数,即可求出∠ACD的度数.
解答 解: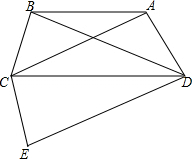 以CD为对称轴作△CDE与△CBD对称,
以CD为对称轴作△CDE与△CBD对称,
则∠DEC=∠DBC,CE=CB,
∵∠DAC=98°,∠DBC=82°,
∴∠DEC=82°,
∴∠DEC+∠DAC=180°,
∴A、D、E、C四点共圆,
∵BC=AD,CE=CB,
∴CE=AD,
∴∠DCA=∠CDE=∠CDB,
∵∠BCD=70°,∠DBC=82°,
∴∠BDC=180°-∠BCD-∠DBC=28°,
∴∠ACD=∠BDC=28°.
故答案为:28°.
点评 本题考查了四点共圆的知识:将四点连成一个四边形,若对角互补,那么这四点共圆,解答本题的关键是根据题目所给的角的度数求出∠DEC+∠DAC=180°,继而得出A、D、E、C四点共圆.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
2.下列计算正确的是( )
| A. | x2+x=2x2 | B. | (-a2)4=-a12 | C. | (3a3)2=9a6 | D. | x11÷x4•x2=x8 |
6.若三角形的两边长为2和5,则第三边长m可以是( )
| A. | 3 | B. | 4.1 | C. | 7 | D. | 11 |
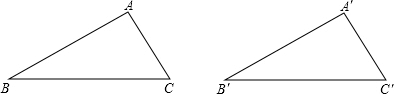

 如图,直线a∥b,AC⊥BC,∠C=90°,∠2=65°,则∠1=25°.
如图,直线a∥b,AC⊥BC,∠C=90°,∠2=65°,则∠1=25°.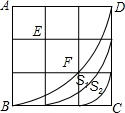 如图,在3×3方格表中,分别以A、E、F为圆心,半径为3,2,1,圆心角都是90°的三段圆弧与正方形ABCD的边界围成了两个带型,那么这两个带型的面积之比S1:S2=5:3.
如图,在3×3方格表中,分别以A、E、F为圆心,半径为3,2,1,圆心角都是90°的三段圆弧与正方形ABCD的边界围成了两个带型,那么这两个带型的面积之比S1:S2=5:3.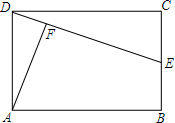 如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,证明△AFD∽△DCE,并计算点A至直线DE的距离(精确到0.1)
如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,证明△AFD∽△DCE,并计算点A至直线DE的距离(精确到0.1)