题目内容
5.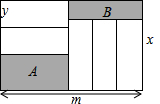 如图,长为m,宽为x(m>x)的大长方形被分割成7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为y,记阴影A与B的面积差为S.
如图,长为m,宽为x(m>x)的大长方形被分割成7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为y,记阴影A与B的面积差为S.(1)分别用含m,x,y的代数式表示阴影A,B的面积,并计算S;
(2)当m=6,y=1时,求S的值;
(3)当x取任何实数时,面积差S的值都保持不变,问m与y应满足什么条件?
分析 (1)找出阴影A中的长与宽,表示出A的面积,找出阴影B中的长与宽,表示出B的面积,由A-B表示出S即可;
(2)把m与y的值代入计算即可求出S的值;
(3)S变形后,根据结果与x值无关确定出m与y的关系式即可.
解答 解:(1)阴影A的面积为(m-3y)(x-2y)=6y2-(2m+3)y+mx,
阴影B面积为3y(x-m+3y)=9y2-3my+3xy,
则S=[6y2-(2m+3)y+mx]-(9y2-3my+3xy)=-3y2+my-6xy+mx;
(2)当m=6,y=1时,S=-3+6+6x-6xx=3;
(3)S=(m-6y)x-3y2+my,
由结果与x无关,得到m-6y=0,
整理得:m=6y.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
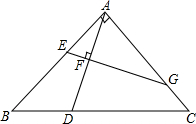 如图,等腰三角形ABC中,∠BAC=90°,AB=AC,点D在BC上,点F在AD上,过点F作EG⊥AD,交AB于E,AC于G,猜测AE,AG,BD,BC之间是否成比例,并说明理由.
如图,等腰三角形ABC中,∠BAC=90°,AB=AC,点D在BC上,点F在AD上,过点F作EG⊥AD,交AB于E,AC于G,猜测AE,AG,BD,BC之间是否成比例,并说明理由. 如图,直线a∥b,AC⊥BC,∠C=90°,∠2=65°,则∠1=25°.
如图,直线a∥b,AC⊥BC,∠C=90°,∠2=65°,则∠1=25°.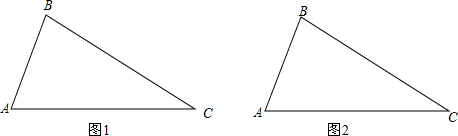
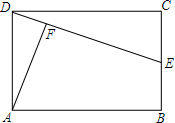 如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,证明△AFD∽△DCE,并计算点A至直线DE的距离(精确到0.1)
如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,证明△AFD∽△DCE,并计算点A至直线DE的距离(精确到0.1) 如图,△ABC≌△BAD,BC=AD.
如图,△ABC≌△BAD,BC=AD.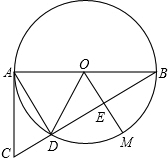 如图,⊙O是△ABD的外接圆,AB是⊙O的直径,M为⊙O上一点,OM⊥BC,垂足为E,点C在BD的延长线上,连接CA,∠CAD=∠CBA
如图,⊙O是△ABD的外接圆,AB是⊙O的直径,M为⊙O上一点,OM⊥BC,垂足为E,点C在BD的延长线上,连接CA,∠CAD=∠CBA