题目内容
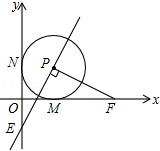 已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0)
已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0)(1)若点E在y轴的负半轴上(如图所示),求证:PE=PF;
(2)在点F运动过程中,设OE=a,OF=b,试用含a的代数式表示b.
考点:圆的综合题
专题:
分析:(1)连接PM,PN,运用△PMF≌△PNE证明;
(2)分两种情况①当t>1时,点E在y轴的负半轴上,0<t≤1时,点E在y轴的正半轴或原点上,再根据(1)求解.
(2)分两种情况①当t>1时,点E在y轴的负半轴上,0<t≤1时,点E在y轴的正半轴或原点上,再根据(1)求解.
解答:(1)证明:如图,连接PM,PN,
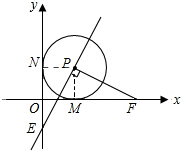
∵⊙P与x轴,y轴分别相切于点M和点N,
∴PM⊥MF,PN⊥ON且PM=PN,
∴∠PMF=∠PNE=90°且∠NPM=90°,
∵PE⊥PF,
∠NPE=∠MPF=90°-∠MPE,
在△PMF和△PNE中,
,
∴△PMF≌△PNE(ASA),
∴PE=PF;
(2)解:分两种情况:
①当t>1时,点E在y轴的负半轴上,如图1,
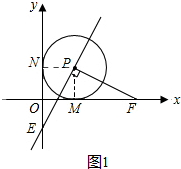
由(1)得△PMF≌△PNE,
∴NE=MF=t,PM=PN=1,
∴b=OF=OM+MF=1+t,a=NE-ON=t-1,
∴b-a=1+t-(t-1)=2,
∴b=2+a,
②0<t≤1时,如图2,点E在y轴的正半轴或原点上,
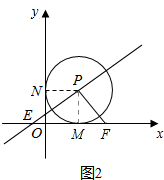
同理可证△PMF≌△PNE,
∴b=OF=OM+MF=1+t,a=OE=ON-NE=1-t,
∴b+a=1+t+1-t=2,
∴b=2-a.
综上所述,当t>1时,b=2+a;当0<t≤1时,b=2-a.

∵⊙P与x轴,y轴分别相切于点M和点N,
∴PM⊥MF,PN⊥ON且PM=PN,
∴∠PMF=∠PNE=90°且∠NPM=90°,
∵PE⊥PF,
∠NPE=∠MPF=90°-∠MPE,
在△PMF和△PNE中,
|
∴△PMF≌△PNE(ASA),
∴PE=PF;
(2)解:分两种情况:
①当t>1时,点E在y轴的负半轴上,如图1,

由(1)得△PMF≌△PNE,
∴NE=MF=t,PM=PN=1,
∴b=OF=OM+MF=1+t,a=NE-ON=t-1,
∴b-a=1+t-(t-1)=2,
∴b=2+a,
②0<t≤1时,如图2,点E在y轴的正半轴或原点上,

同理可证△PMF≌△PNE,
∴b=OF=OM+MF=1+t,a=OE=ON-NE=1-t,
∴b+a=1+t+1-t=2,
∴b=2-a.
综上所述,当t>1时,b=2+a;当0<t≤1时,b=2-a.
点评:本题主要考查了圆的综合题,解题的关键是把圆的知识与全等三角形与相似三角形相结合找出线段关系.

练习册系列答案
相关题目
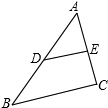 如图所示,在△ABC中,D、E分别是AB,AC上的点,已知AD=4,AB=8,AC=6.下列条件中不能使△ADE∽△ABC的是( )
如图所示,在△ABC中,D、E分别是AB,AC上的点,已知AD=4,AB=8,AC=6.下列条件中不能使△ADE∽△ABC的是( )| A、∠ADE=∠B | ||
| B、∠AED=∠C | ||
| C、AE=3 | ||
D、AE=
|
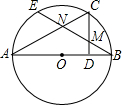 如图,AB为⊙O的直径,C为半圆上一点,且CD⊥AB于点B,E为
如图,AB为⊙O的直径,C为半圆上一点,且CD⊥AB于点B,E为