题目内容
已知点P(3,2)、点Q(-2,a)都在反比例函数y=
的图象上,过点P分别作两坐标轴的垂线,垂线与两坐标轴围成的矩形面积为S1;过点Q分别作两坐标轴的垂线,垂线与两坐标轴围成的矩形面积为S2,求a,S1,S2的值.
| k |
| x |
考点:反比例函数系数k的几何意义
专题:计算题
分析:先根据反比例函数图象上点的坐标特征得到k=3×2=-2×a,易得k=6,a=-3,然后根据反比例函数的比例系数k的几何意义求S1,S2的值.
解答:解:∵点P(3,2)、点Q(-2,a)都在反比例函数y=
的图象上,
∴k=3×2=-2×a,
∴k=6,a=-3,
∵过点P分别作两坐标轴的垂线,垂线与两坐标轴围成的矩形面积为S1;过点Q分别作两坐标轴的垂线,垂线与两坐标轴围成的矩形面积为S2,
∴S1=S2=|6|=6.
| k |
| x |
∴k=3×2=-2×a,
∴k=6,a=-3,
∵过点P分别作两坐标轴的垂线,垂线与两坐标轴围成的矩形面积为S1;过点Q分别作两坐标轴的垂线,垂线与两坐标轴围成的矩形面积为S2,
∴S1=S2=|6|=6.
点评:本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
| k |
| x |

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
下列四个数中最小的是( )
| A、0 | ||
| B、0.5 | ||
| C、-1 | ||
D、
|
下列说法中,正确的有( )
①射线与其反向延长线成一条直线;
②直线a,b相交于点m;
③两直线交于两点;
④三条直线两两相交,一定有3个交点.
①射线与其反向延长线成一条直线;
②直线a,b相交于点m;
③两直线交于两点;
④三条直线两两相交,一定有3个交点.
| A、3个 | B、2个 | C、1个 | D、0个 |
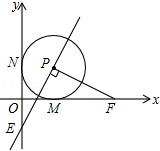 已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0)
已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0) 已知AB,AC为弦,OM⊥AB于M,ON⊥AC于N,求证:MN∥BC且MN=
已知AB,AC为弦,OM⊥AB于M,ON⊥AC于N,求证:MN∥BC且MN=