题目内容
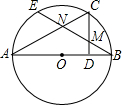 如图,AB为⊙O的直径,C为半圆上一点,且CD⊥AB于点B,E为
如图,AB为⊙O的直径,C为半圆上一点,且CD⊥AB于点B,E为 |
| AC |
CD分别相交于N、M.求证:△CMN为等腰三角形.
考点:圆周角定理,等腰三角形的判定,圆心角、弧、弦的关系
专题:证明题
分析:连接OE交AC于点G,则OE⊥AC,在Rt△EGN和Rt△BDM中,可得∠E+∠ENG=90°,∠B+∠BMD=90°,且∠E=∠B,可得出∠ENG=∠BMD,即可得出∠CNM=∠CMN,所有可得出CN=CM,证得结论.
解答: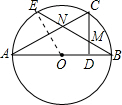
证明:
连接OE交AC于点G,
∵E为
的中点,
∴OE⊥AC,
∴∠E+∠ENG=90°,
∵CD⊥AB于点B,
∴∠B+∠BMD=90°,
∴∠ENG=∠BMD,
又∠ENG=∠CNM,∠BMD=∠CMN,
∴∠CNM=∠CMN,
∴CN=CM,
∴△CMN为等腰三角形.

证明:
连接OE交AC于点G,
∵E为
 |
| AC |
∴OE⊥AC,
∴∠E+∠ENG=90°,
∵CD⊥AB于点B,
∴∠B+∠BMD=90°,
∴∠ENG=∠BMD,
又∠ENG=∠CNM,∠BMD=∠CMN,
∴∠CNM=∠CMN,
∴CN=CM,
∴△CMN为等腰三角形.
点评:本题主要考查垂径定理及等腰三角形的判定和性质,由条件得到OE⊥AC是解题的关键.

练习册系列答案
相关题目
 已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程ax2+bx-c=0是关于x的一元二次方程.
已知△ABC中,a、b、c分别为∠A、∠B、∠C的对边,方程ax2+bx-c=0是关于x的一元二次方程.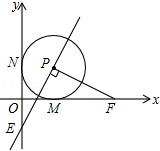 已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0)
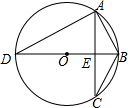
已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0) 已知AB,AC为弦,OM⊥AB于M,ON⊥AC于N,求证:MN∥BC且MN=
已知AB,AC为弦,OM⊥AB于M,ON⊥AC于N,求证:MN∥BC且MN= 如图,菱形ABCD中,对角线AC与BD相交于点O,点E,F,M,N分别为四边的中点,试说明:E,F,M,N四点在同一个圆上.
如图,菱形ABCD中,对角线AC与BD相交于点O,点E,F,M,N分别为四边的中点,试说明:E,F,M,N四点在同一个圆上.