题目内容
规律是数学研究的重要内容之一.初中数学中研究的规律主要有一些特定的规则、符号(数)及其运算规律、图形的数值特征和位置关系特征等方面.请你解决以下与数的表示和运算相关的问题:
(1)在围棋盒中有x颗黑色棋子和y颗白色棋子,从盒中随机取出一个棋子,如果它是黑色棋子的概率是
,写出y用x表示的式子;
(2)在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,Rt△ABC的内切圆半径为r.写出r用a、b、c表示的式子;
(3)函数的研究中,应关注y随x变化而变化的数值规律(课本里研究函数图象的特征实际上也是为了说明函数的数值规律).下面对函数y=x2的某种数值变化规律进行初步研究:
由表看出,当x的取值从0开始每增加1个单位时,y的值依次增加1,3,5…请回答:
①当x的取值从0开始每增加
个单位时,y的值变化规律是什么?
②当x的取值从0开始每增加
个单位时,y的值变化规律是什么?
(1)在围棋盒中有x颗黑色棋子和y颗白色棋子,从盒中随机取出一个棋子,如果它是黑色棋子的概率是
| 3 |
| 8 |
(2)在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,Rt△ABC的内切圆半径为r.写出r用a、b、c表示的式子;
(3)函数的研究中,应关注y随x变化而变化的数值规律(课本里研究函数图象的特征实际上也是为了说明函数的数值规律).下面对函数y=x2的某种数值变化规律进行初步研究:
| xi | 0 | 1 | 2 | 3 | 4 | 5 | … |
| yi | 0 | 1 | 4 | 9 | 16 | 25 | … |
| yi+1-yi | 1 | 3 | 5 | 7 | 9 | 11 | … |
①当x的取值从0开始每增加
| 1 |
| 2 |
②当x的取值从0开始每增加
| 1 |
| n |
考点:二次函数综合题,三角形的内切圆与内心,概率公式
专题:
分析:(1)由概率得出等式关系,进行整理即可得;
(2)设AB、BC、AC与⊙O的切点分别为D、E、F;易证得四边形OECF是正方形;那么根据切线长定理可得:CE=CF=
(AC+BC-AB),由此可求出r的长;
(3)根据图表计算出相应的数值后即可看出y随着x的变化而变化的规律.
(2)设AB、BC、AC与⊙O的切点分别为D、E、F;易证得四边形OECF是正方形;那么根据切线长定理可得:CE=CF=
| 1 |
| 2 |
(3)根据图表计算出相应的数值后即可看出y随着x的变化而变化的规律.
解答:解:(1)黑色棋子的概率=
=
,
整理得y=
x;
(2) 如右图;
如右图;
四边形OECF中,OE=OF,∠OEC=∠OFC=∠C=90°;
∴四边形OECF是正方形;
由切线长定理,得:AD=AF,BD=BE,CE=CF;
∴CE=CF=r=
(a+b-c);
(3)①当x=0时,y=0,
当x=
时,y=
,
当x=1时,y=1,
当x=
时,y=
.
故当x的取值从0开始每增加
个单位时,y的值依次增加
、
、
…
②当x=0时,y=0,
当x=
时,y=
,
当x=
时,y=
,
当x=
时,y=
,
故当x的取值从0开始每增加
个单位时,y的值依次增加
、
、
…
| x |
| x+y |
| 3 |
| 8 |
整理得y=
| 5 |
| 3 |
(2)
 如右图;
如右图;四边形OECF中,OE=OF,∠OEC=∠OFC=∠C=90°;
∴四边形OECF是正方形;
由切线长定理,得:AD=AF,BD=BE,CE=CF;
∴CE=CF=r=
| 1 |
| 2 |
(3)①当x=0时,y=0,
当x=
| 1 |
| 2 |
| 1 |
| 4 |
当x=1时,y=1,
当x=
| 3 |
| 2 |
| 9 |
| 4 |
故当x的取值从0开始每增加
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
②当x=0时,y=0,
当x=
| 1 |
| n |
| 1 |
| n2 |
当x=
| 2 |
| n |
| 4 |
| n2 |
当x=
| 3 |
| n |
| 9 |
| n2 |
故当x的取值从0开始每增加
| 1 |
| n |
| 1 |
| n2 |
| 3 |
| n2 |
| 5 |
| n2 |
点评:此题主要考查概率公式,直角三角形内切圆的性质及半径的求法,二次函数的性质及实数的性质,解题的关键是发现规律并利用规律解题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图,AB与⊙O切于点B,AO=5cm,AB=3cm,则⊙O的半径为( )
如图,AB与⊙O切于点B,AO=5cm,AB=3cm,则⊙O的半径为( )| A、4cm | ||
B、2
| ||
C、2
| ||
D、
|
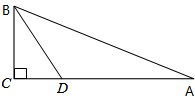
 现有长7m的材料,要制作如图的“目”字形的窗框,为使透过的光最大,则其中一边x应取何值?此时,窗框的面积为多少?
现有长7m的材料,要制作如图的“目”字形的窗框,为使透过的光最大,则其中一边x应取何值?此时,窗框的面积为多少?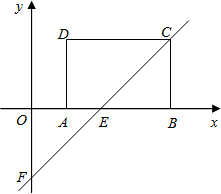 如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.
如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.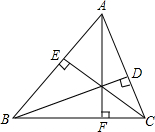 如图,已知AF、BD、CE为△ABC的高.求证:BC2=BE•AB+CD•AC.
如图,已知AF、BD、CE为△ABC的高.求证:BC2=BE•AB+CD•AC.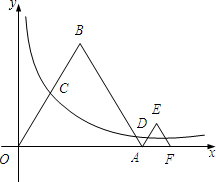 如图,已知等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
如图,已知等边△OAB和等边△AFE的一边都在x轴上,双曲线y=