题目内容
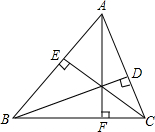如图，已知AF、BD、CE为△ABC的高．求证：BC2=BE•AB+CD•AC．考点：相似三角形的判定与性质
专题：证明题
分析：首先利用相似三角形的判定及其性质表示出线段BF、CF的长度，然后相加即可解决问题．
解答：解：∵AF⊥BC，CE⊥AB，
∴∠AFB=∠CEB；
又∵∠ABF=∠CBE，
∴△ABF∽△CBE，
故
=
，BF=
；
同理可求：CF=
，
∴BF+CF=
，
而BF+CF=BC，
∴BC2=BE•AB+CD•AC．
解：∵AF⊥BC，CE⊥AB，∴∠AFB=∠CEB；
又∵∠ABF=∠CBE，
∴△ABF∽△CBE，
故
| BE |
| BF |
| BC |
| AB |
| BE•AB |
| BC |
同理可求：CF=
| CD•AC |
| BC |
∴BF+CF=
| BE•AB+CD•AC |
| BC |
而BF+CF=BC，
∴BC2=BE•AB+CD•AC．
点评：考查了相似三角形的判定及其性质的应用问题；解题的关键是首先运用分析法将所证明的等式恒等变形，然后运用综合法加以证明．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
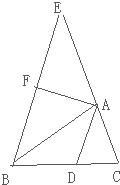
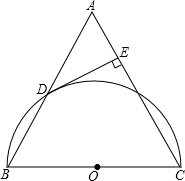已知△ABC中，AB=AC，DE⊥AC于点E，DE与半⊙O相切于点D．
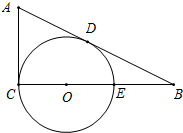在△ABC中，∠ACB=90°，⊙O的圆心O在BC上，交BC于点C、E，且AB切⊙O于D，若OC：CB=1：3，AD=2，求BE．