题目内容
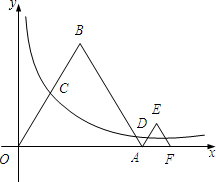 如图,已知等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
如图,已知等边△OAB和等边△AFE的一边都在x轴上,双曲线y=| k |
| x |
(1)求k的值;
(2)等边△AFE的周长.
考点:等边三角形的性质,反比例函数图象上点的坐标特征
专题:
分析:(1)过点C作CM⊥OD于点M,根据等边三角形的性质求出OM、CM的长度,从而得到点C的坐标,再利用待定系数法求反比例函数解析式列式计算即可得解;
(2)过点D作DN⊥AF于点N,设AN=m,根据等边三角形的性质表示出DN的长度,然后表示出点D的坐标,再把点D的坐标代入反比例函数解析式,解方程得到m的值,从而得解.
(2)过点D作DN⊥AF于点N,设AN=m,根据等边三角形的性质表示出DN的长度,然后表示出点D的坐标,再把点D的坐标代入反比例函数解析式,解方程得到m的值,从而得解.
解答:解:(1)如图,

过点C作CM⊥x轴于点M,过点B作BP⊥x于点P,
∴CM∥BP,
∵B点的横坐标为2,点C是等边△OAB的边OB的中点,
∴0M=1,OC=2,∠AOB=60°,
∴CM=
,
∴点C的坐标是(1,
),
由
=
,得:k=
;
(2)连接OD,作DN⊥x轴于点N,
设AN=m,
∴0N=4+m,DN=
m,
∴D点坐标为(4+m,
m),
∴(4+m)•
m=
,
解得m1=
-2,m2=-
-2(舍去);
∴AN=
-2,AD=2
-4;
∴AE=4
-8;
∴等边△AFE的周长为12
-24.

过点C作CM⊥x轴于点M,过点B作BP⊥x于点P,
∴CM∥BP,
∵B点的横坐标为2,点C是等边△OAB的边OB的中点,
∴0M=1,OC=2,∠AOB=60°,
∴CM=
| 3 |
∴点C的坐标是(1,
| 3 |
由
| 3 |
| K |
| 1 |
| 3 |
(2)连接OD,作DN⊥x轴于点N,
设AN=m,
∴0N=4+m,DN=
| 3 |
∴D点坐标为(4+m,
| 3 |
∴(4+m)•
| 3 |
| 3 |
解得m1=
| 5 |
| 5 |
∴AN=
| 5 |
| 5 |
∴AE=4
| 5 |
∴等边△AFE的周长为12
| 5 |
点评:本题是对反比例函数的综合考查,包括待定系数法求反比例函数解析式,等边三角形的性质,解一元二次方程,难度不大,作出辅助线,表示出点C、D的坐标是解题的关键.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
当a=-2时,下列多项式的值为正数的是( )
| A、-a-4 |
| B、-3+a2 |
| C、2a-1 |
| D、a2-4 |
 已知,如图△ABC中,I是内心,AI交BC于D,交△ABC的外接圆于点E,且∠B=60°,那么△IEC是等边三角形吗?说说你的理由.
已知,如图△ABC中,I是内心,AI交BC于D,交△ABC的外接圆于点E,且∠B=60°,那么△IEC是等边三角形吗?说说你的理由.