题目内容
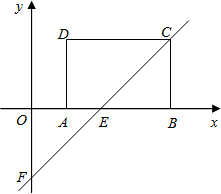 如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.
如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.(1)求:①点D的坐标;
②经过点D,且与直线FC平行的直线的函数表达式;
(2)直线y=x-2上是否存在点P,使得△PDC为等腰直角三角形?若存在,求出点P 的坐标;若不存在,请说明理由.
(3)在平面直角坐标系内确定点M,使得以点M、D、C、E为顶点的四边形是平行四边形,请直接写出点M的坐标.
考点:一次函数综合题
专题:压轴题
分析:(1)①设点C的坐标为(m,2),根据一次函数图象上点的坐标特征,代入直线解析式求解即可得到m的值,再根据矩形的长求出OA,然后写出点D的坐标即可;
②根据互相平行的直线的解析式的k值相等设出直线解析式为y=x+b,然后把点D的坐标代入函数解析式求解即可;
(2)根据直线解析式求出△EBC为等腰直角三角形,根据等腰直角三角形的性质可得∠CEB=∠ECB=45°,再根据平行线的性质可得∠DCE=∠CEB=45°,然后判断出△PDC只能是以P、D为直角顶点的等腰直角三角形,再分①∠D=90°时,根据点P的横坐标与点D的横坐标相等,利用直线解析式求解即可;②∠DPC=90°时,作DC的垂直平分线与直线y=x-2的交点即为点P2,求出点P的横坐标,再代入直线解析式计算即可得解;
(3)根据平行四边形平行且对边相等,分DE、CE是对角线时,点M在x轴上,求出OM的长度,然后写出点M的坐标,CD是对角线时,求出平行四边形的中心的坐标,再求出点E关于中心的对称点,即为点M.
②根据互相平行的直线的解析式的k值相等设出直线解析式为y=x+b,然后把点D的坐标代入函数解析式求解即可;
(2)根据直线解析式求出△EBC为等腰直角三角形,根据等腰直角三角形的性质可得∠CEB=∠ECB=45°,再根据平行线的性质可得∠DCE=∠CEB=45°,然后判断出△PDC只能是以P、D为直角顶点的等腰直角三角形,再分①∠D=90°时,根据点P的横坐标与点D的横坐标相等,利用直线解析式求解即可;②∠DPC=90°时,作DC的垂直平分线与直线y=x-2的交点即为点P2,求出点P的横坐标,再代入直线解析式计算即可得解;
(3)根据平行四边形平行且对边相等,分DE、CE是对角线时,点M在x轴上,求出OM的长度,然后写出点M的坐标,CD是对角线时,求出平行四边形的中心的坐标,再求出点E关于中心的对称点,即为点M.
解答:解:(1)①设点C的坐标为(m,2),
∵点C在直线y=x-2上,
∴2=m-2,
∴m=4,
即点C的坐标为(4,2),
∵四边形ABCD是矩形,
∴AB=CD=3,AD=BC=2,
∴点D的坐标为(1,2);
②设经过点D且与FC平行的直线函数表达式为y=x+b,
将D(1,2)代入y=x+b,得b=1,
∴经过点D且与FC平行的直线函数表达式为y=x+1;
(2)存在.
∵△EBC为等腰直角三角形,
∴∠CEB=∠ECB=45°,
又∵DC∥AB,
∴∠DCE=∠CEB=45°,
∴△PDC只能是以P、D为直角顶点的等腰直角三角形,
如图,①当∠D=90°时,延长DA与直线y=x-2交于点P1,
∵点D的坐标为(1,2),
∴点P1的横坐标为1,
把x=1代入y=x-2得,y=-1,
∴点P1(1,-1);
②当∠DPC=90°时,作DC的垂直平分线与直线y=x-2的交点即为点P2,
所以,点P2的横坐标为
=
,
把x=
代入y=x-2得,y=
,
所以,点P2(
,
),
综上所述,符合条件的点P的坐标为(1,-1)或(
,
);
(3)当y=0时,x-2=0,
解得x=2,
∴OE=2,
∵以点M、D、C、E为顶点的四边形是平行四边形,
∴若DE是对角线,则EM=CD=3,
∴OM=EM-OE=3-2=1,
此时,点M的坐标为(-1,0),
若CE是对角线,则EM=CD=3,
OM=OE+EM=2+3=5,
此时,点M的坐标为(5,0),
若CD是对角线,则平行四边形的中心坐标为(
,2),
设点M的坐标为(x,y),
则
=
,
=2,
解得x=3,y=4,
此时,点M的坐标为(3,4),
综上所述,点M的坐标为(-1,0),(5,0)(3,4).
∵点C在直线y=x-2上,
∴2=m-2,
∴m=4,
即点C的坐标为(4,2),
∵四边形ABCD是矩形,
∴AB=CD=3,AD=BC=2,
∴点D的坐标为(1,2);
②设经过点D且与FC平行的直线函数表达式为y=x+b,
将D(1,2)代入y=x+b,得b=1,
∴经过点D且与FC平行的直线函数表达式为y=x+1;
(2)存在.
∵△EBC为等腰直角三角形,
∴∠CEB=∠ECB=45°,
又∵DC∥AB,
∴∠DCE=∠CEB=45°,
∴△PDC只能是以P、D为直角顶点的等腰直角三角形,
如图,①当∠D=90°时,延长DA与直线y=x-2交于点P1,
∵点D的坐标为(1,2),
∴点P1的横坐标为1,
把x=1代入y=x-2得,y=-1,

∴点P1(1,-1);
②当∠DPC=90°时,作DC的垂直平分线与直线y=x-2的交点即为点P2,
所以,点P2的横坐标为
| 1+4 |
| 2 |
| 5 |
| 2 |
把x=
| 5 |
| 2 |
| 1 |
| 2 |
所以,点P2(
| 5 |
| 2 |
| 1 |
| 2 |
综上所述,符合条件的点P的坐标为(1,-1)或(
| 5 |
| 2 |
| 1 |
| 2 |
(3)当y=0时,x-2=0,
解得x=2,
∴OE=2,
∵以点M、D、C、E为顶点的四边形是平行四边形,
∴若DE是对角线,则EM=CD=3,
∴OM=EM-OE=3-2=1,
此时,点M的坐标为(-1,0),
若CE是对角线,则EM=CD=3,
OM=OE+EM=2+3=5,
此时,点M的坐标为(5,0),
若CD是对角线,则平行四边形的中心坐标为(
| 5 |
| 2 |
设点M的坐标为(x,y),
则
| x+2 |
| 2 |
| 5 |
| 2 |
| y+0 |
| 2 |
解得x=3,y=4,
此时,点M的坐标为(3,4),
综上所述,点M的坐标为(-1,0),(5,0)(3,4).
点评:本题是一次函数综合题型,主要利用了一次函数图象上点的坐标特征,矩形的性质,等腰直角三角形的性质,平行四边形的性质,熟记各性质是解题的关键,难点在于(2)(3)分情况讨论.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
在分别标有号码2、3、4、…10的9个球中,随机取出两个球,记下它们的标号,则较大标号被较小标号整除的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|