题目内容
14.某厂工业废气的年排放量为450万立方米,为改善大气质量环境,决定分两期投入治理,使废气的年排气量减少到288万立方米,如果每期治理中废气减少的百分率相同.(1)求每期减少的百分率是多少?
(2)预计第一期治理中每减少1万立方米需投入3万元,第二期治理中每减少1万立方米废气需投入2.5万元.问两期治理完成后共需投入多少万元?
分析 (1)等量关系为:450×(1-减少的百分率)2=288,把相关数值代入计算即可;
(2)两期治理共需投入资金=第一期减少废气量×3+第二期减少废气量×2.5.
解答 解:(1)设每期减少的百分率是x,
450×(1-x)2=288,
解得:x1=1.8(舍去),x2=0.2
解得x=20%.
答:每期减少的百分率是20%.
(2)两期治理共需投入资金=450×20%×3+(450-450×20%)×20%×2.5=450(万元).
答:两期治理共需投入450万元.
点评 此题主要考查了一元二次方程的应用;求平均变化率的方法为:若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
5.下列等式中正确的是( )
| A. | $\frac{0.1x-0.3y}{0.2x+y}$=$\frac{x-3y}{2x+y}$ | B. | $\frac{x+y}{x-y}$=0 | ||
| C. | $\frac{-x+y}{x-y}$=-1 | D. | $\frac{b}{a}$=$\frac{{b}^{2}}{{a}^{2}}$ |
2.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足下列条件但不是直角三角形的是( )
| A. | a:b:c=5:6:7 | B. | a:b:c=5:4:3 | C. | ∠A=∠B-∠C | D. | ∠A:∠B:∠C=1:1:2 |
9.下列为真命题的是( )
| A. | 相等的角是对顶角 | B. | 两点之间线段最短 | ||
| C. | 两直线平行,同旁内角相等 | D. | 若$\sqrt{{a}^{2}}$=a,则a>0 |
19.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | C. | $\sqrt{2}$$•\sqrt{3}$=$\sqrt{6}$ | D. | $\sqrt{8}$$÷\sqrt{2}$=4 |
4.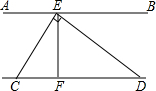 如图,AB∥CD,∠CED=90°,EF⊥CD,F为垂足,则图中与∠EDF互余的角有( )
如图,AB∥CD,∠CED=90°,EF⊥CD,F为垂足,则图中与∠EDF互余的角有( )
 如图,AB∥CD,∠CED=90°,EF⊥CD,F为垂足,则图中与∠EDF互余的角有( )
如图,AB∥CD,∠CED=90°,EF⊥CD,F为垂足,则图中与∠EDF互余的角有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |