题目内容
9.若a,b为相邻整数,且a<$\sqrt{5}$<b,则b-a=$\frac{1}{9}$.分析 估算$\sqrt{5}$的范围,即可确定a,b的值,即可解答.
解答 解:∵$2<\sqrt{5}<3$,且<$\sqrt{5}$<b,
∴a=2,b=3,
∴b-a=${3}^{-2}=\frac{1}{9}$,
故答案为:$\frac{1}{9}$.
点评 本题考查了估算无理数的方法:找到与这个数相邻的两个完全平方数,这样就能确定这个无理数的大小范围.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | C. | $\sqrt{2}$$•\sqrt{3}$=$\sqrt{6}$ | D. | $\sqrt{8}$$÷\sqrt{2}$=4 |
4.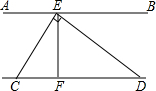 如图,AB∥CD,∠CED=90°,EF⊥CD,F为垂足,则图中与∠EDF互余的角有( )
如图,AB∥CD,∠CED=90°,EF⊥CD,F为垂足,则图中与∠EDF互余的角有( )
 如图,AB∥CD,∠CED=90°,EF⊥CD,F为垂足,则图中与∠EDF互余的角有( )
如图,AB∥CD,∠CED=90°,EF⊥CD,F为垂足,则图中与∠EDF互余的角有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
19.已知分式$\frac{x-1}{{x}^{2}+2}$有意义,则x的取值应满足( )
| A. | x可取任何实数 | B. | x≠1 | C. | x≥1 | D. | -2<x<1 |