题目内容
2.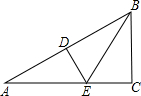 如图,在△ABC中,∠C=90°,DE⊥AB于D,BC=BD,若AC=4cm,则AE+DE=4cm.
如图,在△ABC中,∠C=90°,DE⊥AB于D,BC=BD,若AC=4cm,则AE+DE=4cm.
分析 由条件可证明Rt△CBE≌Rt△DBE,则可求得DE=EC,可求得答案.
解答 解:
∵DE⊥AB,
∴∠C=∠BDE,
在Rt△CBE和Rt△DBE中
$\left\{\begin{array}{l}{BE=BE}\\{BC=BD}\end{array}\right.$
∴Rt△CBE≌Rt△DBE(HL),
∴CE=DE,
∴AE+DE=AE+CE=AC=4cm,
故答案为:4cm.
点评 本题主要考查全等三角形的判定和性质,证得Rt△CBE≌Rt△DBE得到CE=DE是解题的关键.

练习册系列答案
相关题目
19.下列运算正确的是( )
| A. | a6÷a2=a3 | B. | a5-a2=a3 | ||
| C. | (3a3)2=6a9 | D. | 2(a3b)2-3(a3b)2=-a6b2 |
3.已知正方形的边长a(cm)
(1)正方形的面积S(cm2)与边长a(cm)的函数关系式为a2
(2)用表格表示:
(3)用图象表示:
(4)根据以上三种表示方法回答问题;
①自变量的取值范围是什么?
②如何描述S随a的变化而变化的惰况?
(1)正方形的面积S(cm2)与边长a(cm)的函数关系式为a2
(2)用表格表示:
| a/m | … | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | … |
| cm 2 | … | … |
(4)根据以上三种表示方法回答问题;
①自变量的取值范围是什么?
②如何描述S随a的变化而变化的惰况?
12.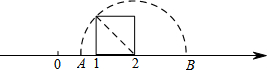 如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是( )
如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是( )
 如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是( )
如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是( )| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$-1 | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-$\frac{1}{2}$ |
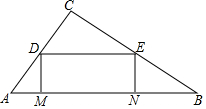 如图,△ABC中,∠C=90°,AC=3,BC=4,在线段AB上,动点M从点A出发向点B做匀速运动,同时动点N从B出发向点A做匀速运动,当点M、N其中一点停止运动时,另一点也停止运动,分别过点M、N做AB的垂线,分别交两直角边于点D、E,连接DE,若运动时间为t秒,在运动过程中四边形DENM总为矩形(点M、N重合除外).
如图,△ABC中,∠C=90°,AC=3,BC=4,在线段AB上,动点M从点A出发向点B做匀速运动,同时动点N从B出发向点A做匀速运动,当点M、N其中一点停止运动时,另一点也停止运动,分别过点M、N做AB的垂线,分别交两直角边于点D、E,连接DE,若运动时间为t秒,在运动过程中四边形DENM总为矩形(点M、N重合除外). 如图,在△ABC中,BD=CD,BE交AD于F,AE=EF,若BE=7CE,AE=$\frac{5}{2}$,则BF=$\frac{10}{3}$.
如图,在△ABC中,BD=CD,BE交AD于F,AE=EF,若BE=7CE,AE=$\frac{5}{2}$,则BF=$\frac{10}{3}$. 已知数a,b,c在数轴上位置如图,
已知数a,b,c在数轴上位置如图,