题目内容
3．已知正方形的边长a（cm）（1）正方形的面积S（cm2）与边长a（cm）的函数关系式为a2
（2）用表格表示：
| a/m | … | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | … |
| cm 2 | … | … |
（4）根据以上三种表示方法回答问题；
①自变量的取值范围是什么？
②如何描述S随a的变化而变化的惰况？
分析 （1）根据正方形的面积公式可知：S=a2．
（2）把自变量的值代入求出函数值即可．
（3）画出函数图象即可．
（4）①根据实际意义以及函数表达式即可确定自变量的取值范围．
②观察图象可知S随a增加而增加．
解答 解：（1）S=a2．
（2）答案分别为$\frac{1}{4}$，1，$\frac{9}{4}$，4，$\frac{25}{4}$，9．
（3）函数图象如图所示，
（4）①在便利店取值范围是a＞0．
②S随a增加而增加．
点评 本题考查函数关系式、正方形的面积公式、函数值，自变量等知识，解题的关键是理解题意，掌握基本概念．
练习册系列答案
相关题目
13．化简$\frac{{x}^{2}}{x-1}$-x+1的结果是（ ）
| A． | $\frac{1}{x-1}$ | B． | $\frac{1}{1-x}$ | C． | $\frac{1-2x}{x-1}$ | D． | $\frac{2x-1}{x-1}$ |
如图，已知直线y=3x-3分别交x轴、y轴于A、B两点，抛物线y=x2+bx+c经过
如图，在△ABC中，∠C=90°，DE⊥AB于D，BC=BD，若AC=4cm，则AE+DE=4cm．
6．下列关于平方根说法和等式中正确的是（ ）
| A． | $\sqrt{\frac{4}{25}}=±\frac{2}{5}$ | B． | $\sqrt{{{（{-3}）}^2}}=-3$ | C． | -a2没有平方根 | D． | $-\sqrt{{{（{-4}）}^2}}=-4$ |
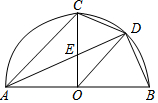如图AB是半圆直径，半径OC⊥AB于点O，AD平分∠CAB分别交OC于点E，交弧BC于点D，连结CD、OD，给出以下5个结论：