��Ŀ����
8��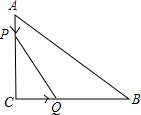 ��ͼ����ABC�У���C=90�㣬AC=6cm��BC=8cm����P��A��AC����C����1cm/s���ٶ��ƶ�����C��ֹͣ����Q��C�㿪ʼ��CB�����B��2cm/s���ٶ��ƶ�����B��ֹͣ��
��ͼ����ABC�У���C=90�㣬AC=6cm��BC=8cm����P��A��AC����C����1cm/s���ٶ��ƶ�����C��ֹͣ����Q��C�㿪ʼ��CB�����B��2cm/s���ٶ��ƶ�����B��ֹͣ����1�������P��Q�ֱ��A��Cͬʱ���������������ӣ�ʹS��QPC=8cm2��
��2�������P�ӵ�A�ȳ���2s����Q�ٴӵ�C���������������Ӻ�S��QPC=4cm2��
��3�������P��Q�ֱ��A��Cͬʱ���������������Ӻ�PQ=BQ��
���� �������P����xs��S��QPC������֪������
�ڣ�1���У�AP=xm��PC=��6-x��m��QC=2xm��
�ڣ�2���У�AP=xm��PC=��6-x��m��QC=2��x-2��m���������г����̣�����𰸣�
�ڣ�3���У�PC=��6-x��m��QC=2xm��BQ=8-2x�����ù��ɶ�����PQ=BQ�г����̣�����𰸣�
��� �⣺��1��P��Qͬʱ����������x���ӣ�S��QPC=8cm2��������ã�
$\frac{1}{2}$��6-x��•2x=8��
��x2-6x+8=0��
��ã�x1=2��x2=4��
��2���P����A��1��2=2cm������Q��C��2��2=4cm������4s��P����A��1��4=4cm������Q��C��2��4=8cm��������֤�����Ƕ�����Ҫ��
��P��Qͬʱ����������2s��4s��S��QPC=8cm2��
��2����P����tsʱS��QPC=4cm2����Q�˶���ʱ��Ϊ��t-2���룬������ã�
$\frac{1}{2}$��6-t��•2��t-2��=4��
��t2-8t+16=0��
��ã�t1=t2=4
��˾�4���P��A��1��4=4cm����Q��C��2����4-2��=4cm���������⣮
��P�ȳ���2s��Q�ٴ�C����2s��S��QPC=4cm2��
��3���辭��x���Ӻ�PQ=BQ����PC=��6-x��m��QC=2xm��BQ=8-2x��
��6-x��2+��2x��2=��8-2x��2��
���x1=-10+8$\sqrt{2}$��x2=-10-8$\sqrt{2}$���������⣬��ȥ��
�𣺾���-10+8$\sqrt{2}$���Ӻ�PQ=BQ��
���� ���⿼��һԪ���η��̵�ʵ�����ã�����Ĺؼ���Ū��ͼ����ʵ������Ĺ�ϵ�����⣬��Ҫע���ĺ����ԣ��Ӷ�ȷ��ȡ�ᣮ

 ���Ž�����ٰθ��νӹ㶫���������ϵ�д�
���Ž�����ٰθ��νӹ㶫���������ϵ�д� �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д� ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д�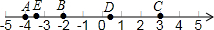 ������ͼ��ʾ�����ᣬ�����б���������ָ����һ���ʾ�����ľ���ֵ���
������ͼ��ʾ�����ᣬ�����б���������ָ����һ���ʾ�����ľ���ֵ���| �� | A | B | C | D | E |
| ������ | -4 | -2 | 0.5 | ||
| �෴�� | 2 | -3 | |||
| ����ֵ | 4 | 3.5 |
| A�� | 2��3��$\sqrt{13}$��һ�鹴���� | |
| B�� | �����$\sqrt{5}$$��\root{3}{7}$ | |
| C�� | �������������� | |
| D�� | �ں�����֪��һ����λ�ǾͿ���ȷ��һ��Ŀ���λ�� |
| A�� | ���е�ֱ�������ζ����� | B�� | ���еĵ��������ζ����� | ||
| C�� | ���еĵ���ֱ�������ζ����� | D�� | ���еľ��ζ����� |
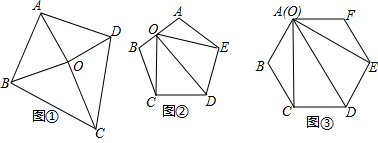
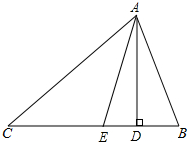 ��ͼ���ڡ�ABC�У���B����C��AD�Ǹߣ�AE�ǽ�ƽ���ߣ������DAE���B�͡�C�Ĺ�ϵ����˵�����ɣ�
��ͼ���ڡ�ABC�У���B����C��AD�Ǹߣ�AE�ǽ�ƽ���ߣ������DAE���B�͡�C�Ĺ�ϵ����˵�����ɣ�