题目内容
9. 如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线DE交AC于点E,交BC于点D,求证:BD=2DC.
如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线DE交AC于点E,交BC于点D,求证:BD=2DC.
分析 先根据等腰三角形的性质求出∠B及∠C的度数,再由线段垂直平分线的性质得出AD=CD,∠DAC=∠C,由此可得出∠BAD的度数,由直角三角形的性质即可得出结论.
解答 证明:∵在△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠C=$\frac{180°-120°}{2}$=30°.
∵AC的垂直平分线DE交AC于点E,
∴AD=CD,∠DAC=∠C=30°,
∴∠BAD=∠BAC-∠DAC=120°-30°=90°,
∴BD=2AD,
∴BD=2DC.
点评 本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
19.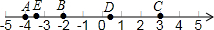 根据如图所示的数轴,把下列表格补充完整,指出哪一点表示的数的绝对值最大.
根据如图所示的数轴,把下列表格补充完整,指出哪一点表示的数的绝对值最大.
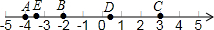 根据如图所示的数轴,把下列表格补充完整,指出哪一点表示的数的绝对值最大.
根据如图所示的数轴,把下列表格补充完整,指出哪一点表示的数的绝对值最大.| 点 | A | B | C | D | E |
| 有理数 | -4 | -2 | 0.5 | ||
| 相反数 | 2 | -3 | |||
| 绝对值 | 4 | 3.5 |
20.下列叙述正确的是( )
| A. | 所有的直角三角形都相似 | B. | 所有的等腰三角形都相似 | ||
| C. | 所有的等腰直角三角形都相似 | D. | 所有的矩形都相似 |
14.已知等腰三角形的一边长是9cm,另一边长是5cm,那么这个等腰三角形的周长是( )
| A. | 19cm | B. | 23cm | C. | 16cm | D. | 19cm或23cm |
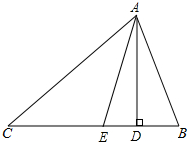 如图,在△ABC中,∠B>∠C,AD是高,AE是角平分线.猜想∠DAE与∠B和∠C的关系,并说明理由.
如图,在△ABC中,∠B>∠C,AD是高,AE是角平分线.猜想∠DAE与∠B和∠C的关系,并说明理由.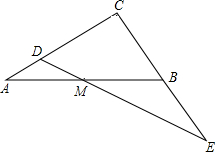 如图,已知△ABC,∠ACB=90°,BC=AC=1,M为边AB中点,D为AC边上任意一点,联结DM并延长与CB延长线交于点E.设AD=x,BE=y.
如图,已知△ABC,∠ACB=90°,BC=AC=1,M为边AB中点,D为AC边上任意一点,联结DM并延长与CB延长线交于点E.设AD=x,BE=y.