题目内容
20．定义函数y=[x•[x]]，其中[x]表示不超过x的最大整数，如：[1.5]=1，[-1.3]=-2．当x∈[0，n）（n∈N*）时，记an为函数y的所有可能取值的个数．则a10=（ ）| A． | 45 | B． | 46 | C． | 55 | D． | 66 |
分析 先由题意求出[x]，再求x[x]，然后求出[x[x]]，得到an．
解答 解：由题意可得：[x]=$\left\{\begin{array}{l}{0，0≤x＜1}\\{1，1≤x＜2}\\{…}\\{n-1，n-1≤x＜n}\end{array}\right.$，
∴x[x]=$\left\{\begin{array}{l}{0，0≤x＜1}\\{x，1≤x＜2}\\{…}\\{（n-1）x，n-1≤x＜n}\end{array}\right.$，
∴[x[x]]在各区间中元素的个数是：1，1，2，3，…，n-1，
∴an=$\frac{n（n-1）}{2}$+1，
则a10=$\frac{10×9}{2}$+1=46．
故选：B．
点评 此题主要考查了取整计算，根据题意分段得出各区间中元素的个数是解题关键．
练习册系列答案
相关题目
8．△ABC中，点D在边BC上，已知AB=AD=2，AC=4，且BD：DC=2：3，则△ABC是（ ）
| A． | 锐角三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 无法确定 |
15．
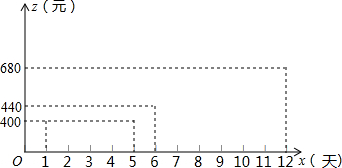在“春季经贸洽谈会”上，我市某服装厂接到生产一批出口服装的订单，要求必须在12天（含12天）内保质保量完成，且当天加工的服装当天立即空运走．为了加快进度，车间采取工人轮流休息，机器满负荷运转的生产方式，生产效率得到了提高．这样每天生产的服装数量y（套）与时间x（元）的关系如表：
由于机器损耗等原因，当每天生产的服装数达到一定量后，平均每套服装的成本会随着服装产量的增加而增大，这样平均每套服装的成本z（元）与生产时间x（天）的关系如图所示．
（1）判断每天生产的服装的数量y（套）与生产时间x（元）之间是我们学过的哪种函数关系？并验证．
（2）已知这批外贸服装的订购价格为每套1570元，设车间每天的利润为w（元）．求w（元）与x（天）之间的函数关系式，并求出哪一天该生产车间获得最高利润，最高利润是多少元？
（3）从第6天起，该厂决定该车间每销售一套服装就捐a元给山区的留守儿童作为建图书室的基金，但必须保证每天扣除捐款后的利润随时间的增大而增大．求a的最大值，此时留守儿童共得多少元基金？
在“春季经贸洽谈会”上，我市某服装厂接到生产一批出口服装的订单，要求必须在12天（含12天）内保质保量完成，且当天加工的服装当天立即空运走．为了加快进度，车间采取工人轮流休息，机器满负荷运转的生产方式，生产效率得到了提高．这样每天生产的服装数量y（套）与时间x（元）的关系如表：| 时间x（天） | 1 | 2 | 3 | 4 | … |
| 每天产量y（套） | 22 | 24 | 26 | 28 | … |
（1）判断每天生产的服装的数量y（套）与生产时间x（元）之间是我们学过的哪种函数关系？并验证．
（2）已知这批外贸服装的订购价格为每套1570元，设车间每天的利润为w（元）．求w（元）与x（天）之间的函数关系式，并求出哪一天该生产车间获得最高利润，最高利润是多少元？
（3）从第6天起，该厂决定该车间每销售一套服装就捐a元给山区的留守儿童作为建图书室的基金，但必须保证每天扣除捐款后的利润随时间的增大而增大．求a的最大值，此时留守儿童共得多少元基金？
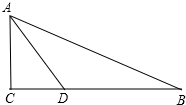在直角三角形ABC中，∠C=90°，AD是∠A的平分线，且CD=$\sqrt{6}$，DB=$2\sqrt{6}$，求△ABC的三边长？