题目内容
3．在5瓶饮料中，有2瓶已过了保质期，随机地从这5瓶饮料中取2瓶，收到至少有1瓶过保质期的饮料的概率为$\frac{7}{10}$．分析 用A、A、A表示没过保质期的饮料，B、B表示过期的饮料，先画树状图展示所有20种等可能的结果数，再找出至少有1瓶过保质期的饮料的结果数，然后根据概率公式求解．
解答 解：用A、A、A表示没过保质期的饮料，B、B表示过期的饮料，
画树状图为：
共有20种等可能的结果数，其中至少有1瓶过保质期的饮料的结果数为14种，
所以取2瓶，收到至少有1瓶过保质期的饮料的概率=$\frac{14}{20}$=$\frac{7}{10}$．
故答案为$\frac{7}{10}$．
点评 本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
18．设直线kx+（k+1）y-1=0（k为正整数）与两坐标轴所围成的三角形面积为Sk，k=1，2，…，2004，那么（S1+S2+…+S2004）等于（ ）
| A． | $\frac{1001}{2004}$ | B． | $\frac{1001}{1002}$ | C． | $\frac{2004}{2005}$ | D． | $\frac{1002}{2005}$ |
8．△ABC中，点D在边BC上，已知AB=AD=2，AC=4，且BD：DC=2：3，则△ABC是（ ）
| A． | 锐角三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 无法确定 |
15．
在“春季经贸洽谈会”上，我市某服装厂接到生产一批出口服装的订单，要求必须在12天（含12天）内保质保量完成，且当天加工的服装当天立即空运走．为了加快进度，车间采取工人轮流休息，机器满负荷运转的生产方式，生产效率得到了提高．这样每天生产的服装数量y（套）与时间x（元）的关系如表：
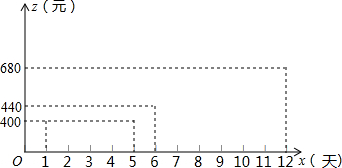
由于机器损耗等原因，当每天生产的服装数达到一定量后，平均每套服装的成本会随着服装产量的增加而增大，这样平均每套服装的成本z（元）与生产时间x（天）的关系如图所示．
（1）判断每天生产的服装的数量y（套）与生产时间x（元）之间是我们学过的哪种函数关系？并验证．
（2）已知这批外贸服装的订购价格为每套1570元，设车间每天的利润为w（元）．求w（元）与x（天）之间的函数关系式，并求出哪一天该生产车间获得最高利润，最高利润是多少元？
（3）从第6天起，该厂决定该车间每销售一套服装就捐a元给山区的留守儿童作为建图书室的基金，但必须保证每天扣除捐款后的利润随时间的增大而增大．求a的最大值，此时留守儿童共得多少元基金？
在“春季经贸洽谈会”上，我市某服装厂接到生产一批出口服装的订单，要求必须在12天（含12天）内保质保量完成，且当天加工的服装当天立即空运走．为了加快进度，车间采取工人轮流休息，机器满负荷运转的生产方式，生产效率得到了提高．这样每天生产的服装数量y（套）与时间x（元）的关系如表：| 时间x（天） | 1 | 2 | 3 | 4 | … |
| 每天产量y（套） | 22 | 24 | 26 | 28 | … |
（1）判断每天生产的服装的数量y（套）与生产时间x（元）之间是我们学过的哪种函数关系？并验证．
（2）已知这批外贸服装的订购价格为每套1570元，设车间每天的利润为w（元）．求w（元）与x（天）之间的函数关系式，并求出哪一天该生产车间获得最高利润，最高利润是多少元？
（3）从第6天起，该厂决定该车间每销售一套服装就捐a元给山区的留守儿童作为建图书室的基金，但必须保证每天扣除捐款后的利润随时间的增大而增大．求a的最大值，此时留守儿童共得多少元基金？