题目内容
阅读下列材料:
1×2=
(1×2×3-0×1×2)
2×3=
(2×3×4-1×2×3)
3×4=
(3×4×5-2×3×4)
由以上三个等式相加,可得1×2+2×3+3×4=
×3×4×5=20
读完以上材料,请你计算下列各题:
(1)1×2+2×3+3×4+…+10×11(仿照以上材料,写出解答过程)
(2)1×2+2×3+3×4+…+n(n+1)= (填上结果即可)
(3)1×2×3+2×3×4+3×4×5+…+n(n+1)(n+2)= (填上结果即可)
1×2=
| 1 |
| 3 |
2×3=
| 1 |
| 3 |
3×4=
| 1 |
| 3 |
由以上三个等式相加,可得1×2+2×3+3×4=
| 1 |
| 3 |
读完以上材料,请你计算下列各题:
(1)1×2+2×3+3×4+…+10×11(仿照以上材料,写出解答过程)
(2)1×2+2×3+3×4+…+n(n+1)=
(3)1×2×3+2×3×4+3×4×5+…+n(n+1)(n+2)=
考点:规律型:数字的变化类
专题:
分析:(1)根据题目信息列出算式,然后提取
,进行计算即可得解;
(2)观察不难发现,两个连续的自然数的积等于这两个数与后面的数的积减去与前面的数的积的
,然后列出算式进行计算即可;
(3)利用(2)的规律类比得出答案即可.
| 1 |
| 3 |
(2)观察不难发现,两个连续的自然数的积等于这两个数与后面的数的积减去与前面的数的积的
| 1 |
| 3 |
(3)利用(2)的规律类比得出答案即可.
解答:解:(1)1×2+2×3+3×4+…+10×11,
=
×(1×2×3-0×1×2)+
×(2×3×4-1×2×3)+
×(3×4×5-2×3×4)+…+
×(10×11×12-9×10×11),
=
×(1×2×3-0×1×2+2×3×4-1×2×3+3×4×5-2×3×4+…+10×11×12-9×10×11),
=
×10×11×12,
=440;
(2)∵1×2+2×3+3×4=
×3×4×5,
∴1×2+2×3+3×4+…+n×(n+1)=
n(n+1)(n+2);
(3)1×2×3+2×3×4+3×4×5+…+n(n+1)(n+2)=
(n+1)(n+2)(n+3).
=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 3 |
=
| 1 |
| 3 |
=440;
(2)∵1×2+2×3+3×4=
| 1 |
| 3 |
∴1×2+2×3+3×4+…+n×(n+1)=
| 1 |
| 3 |
(3)1×2×3+2×3×4+3×4×5+…+n(n+1)(n+2)=
| 1 |
| 4 |
点评:此题考查数字的规律性变化,利用类比的思想由特殊到一般,找出规律,解决问题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
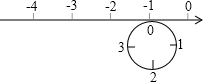 如图,圆的周长为4个单位长度.在该圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上.则数轴上表示-2014的点与圆周上表示数字几的点重合( )
如图,圆的周长为4个单位长度.在该圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上.则数轴上表示-2014的点与圆周上表示数字几的点重合( )| A、0 | B、1 | C、2 | D、3 |
下列四个数中最小的数是( )
| A、5 | ||
B、-
| ||
| C、0 | ||
| D、-2 |
 抛物线y=ax2-4ax+c交x轴于A、B两点,已知A(1,0),抛物线经过点N(4,-3),交y轴于点C.
抛物线y=ax2-4ax+c交x轴于A、B两点,已知A(1,0),抛物线经过点N(4,-3),交y轴于点C.
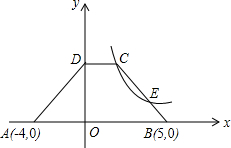 如图,直角坐标内有一个等腰梯形ABCD,DC∥AB,A(-4,0),B(5,0),D在y轴上,C在反比例函数y=
如图,直角坐标内有一个等腰梯形ABCD,DC∥AB,A(-4,0),B(5,0),D在y轴上,C在反比例函数y=