题目内容
有一根20m长的绳子，怎样用它围成一个面积为24m2的矩形？
考点：一元二次方程的应用
专题：几何图形问题
分析：由题意设矩形的长为xm，则宽为（20÷2-x）m，面积为x（10-x），根据题目中矩形面积为24m2，列方程求解即可．
解答：解：设矩形的长为xm，则宽为（20÷2-x）m，由题意得
x（20÷2-x）=24
x（10-x）=24
解得x1=4（不合题意舍去），x2=6，
所以矩形的长为6m，宽为10-6=4m．
答：可以围成一个长6米宽4米的矩形．
x（20÷2-x）=24
x（10-x）=24
解得x1=4（不合题意舍去），x2=6，
所以矩形的长为6m，宽为10-6=4m．
答：可以围成一个长6米宽4米的矩形．
点评：此题主要考查了一元二次方程中长方形面积的应用，表示出矩形两边长，进而得出面积，再解方程是解决本题的关键．
练习册系列答案
相关题目
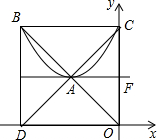如图，点A是过点F（0，2）且和y轴垂直的直线上一点，点O是坐标原点．经过点A作OA的垂线交y轴于点C，以A为顶点且开口向上的抛物线y=a（x-h）2+2经过点C，直线OA交抛物线于另一点B，直线AC交x轴于点D，点A、B均在第二象限且互不重合．
如图，BC⊥AE，垂足为C，过点C作CD∥AB，若∠ECD=51°，则∠B的度数为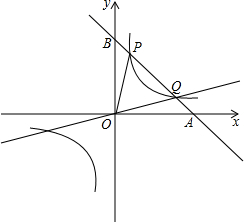
如图，双曲线y1=
下图右边四个图形中是左边展开图的立体图的是（ ）A、 |
B、 |
C、 |
D、 |
用一个经过正方体上、下两面对角线的平面截该正方体，截面是（ ）
| A、三角形 | B、正方形 |
| C、长方形 | D、梯形 |