题目内容
14. 如图,已知点A(1,2)是反比例函数y=$\frac{k}{x}$图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△PAB是等腰三角形,则点P的坐标是(-3,0)或(5,0)或(3,0)或(-5,0).
如图,已知点A(1,2)是反比例函数y=$\frac{k}{x}$图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△PAB是等腰三角形,则点P的坐标是(-3,0)或(5,0)或(3,0)或(-5,0).
分析 由对称性可知O为AB的中点,则当△PAB为等腰三角形时只能有PA=AB或PB=AB,设P点坐标为(x,0),可分别表示出PA和PB,从而可得到关与x的方程,可求得x,可求得P点坐标.
解答 解:
∵反比例函数y=$\frac{k}{x}$图象关于原点对称,
∴A、B两点关于O对称,
∴O为AB的中点,且B(-1,-2),
∴当△PAB为等腰三角形时有PA=AB或PB=AB,
设P点坐标为(x,0),
∵A(1,2),B(-1,-2),
∴AB=$\sqrt{[1-(-1)]^{2}+[2-(-2)]^{2}}$=2$\sqrt{5}$,PA=$\sqrt{(x-1)^{2}+{2}^{2}}$,PB=$\sqrt{(x+1)^{2}+(-2)^{2}}$,
当PA=AB时,则有$\sqrt{(x-1)^{2}+{2}^{2}}$=2$\sqrt{5}$,解得x=-3或5,此时P点坐标为(-3,0)或(5,0);
当PB=AB时,则有$\sqrt{(x+1)^{2}+(-2)^{2}}$=2$\sqrt{5}$,解得x=3或-5,此时P点坐标为(3,0)或(-5,0);
综上可知P点的坐标为(-3,0)或(5,0)或(3,0)或(-5,0),
故答案为:(-3,0)或(5,0)或(3,0)或(-5,0).
点评 本题主要考查等腰三角形的性质和反比例函数的对称性,判断出只有PA=AB或PB=AB两种情况是解题的关键,注意方程思想的应用.

练习册系列答案
相关题目
9.下列事件中,是确定事件的是( )
| A. | 打开电视,它正在播郑州新闻 | B. | 抛掷一枚一元的硬币,正面朝上 | ||
| C. | 367人中有两人的生日相同 | D. | 打雷后会下雨 |
3.已知弹簧在一定限度内,它的长度y(厘米)与所挂重物质量x(千克)是一次函数关系.表中记录的是两次挂不同重量重物的质量(在弹性限度内)与相对应的弹簧长度.
求不挂重物时弹簧的长度.
| 所挂重物质量x(千克) | 2.5 | 5 |
| 弹簧长度y(厘米) | 7.5 | 9 |
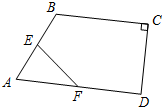 已知:如图,在四边形ABCD中,∠C=90°,E、F分别为AB、AD的中点,BC=6,CD=4,则EF=$\sqrt{13}$.
已知:如图,在四边形ABCD中,∠C=90°,E、F分别为AB、AD的中点,BC=6,CD=4,则EF=$\sqrt{13}$.