题目内容
 如图:AB是半圆的直径,O是圆心,C、D是半圆上的两点,若AB=4,弦AC=CD=1.
如图:AB是半圆的直径,O是圆心,C、D是半圆上的两点,若AB=4,弦AC=CD=1.(1)求证:OC∥BD;
(2)设∠AOC=α,求sinα的值;
(3)求BD的长.
考点:垂径定理,圆心角、弧、弦的关系,解直角三角形
专题:
分析:(1)先根据AC=CD=1可得出
=
,故可得出∠AOC=∠ABD,进而可得出结论;
(2)连接AD,OD,AD和CO相交于E,根据AC=CD,AO=DO可知四边形ACDO的对角线AD和CO互相垂直,由勾股定理可知CE2=AC2-AE2,EO2=AO2-AE2,CE+EO=CO=2,根据AB=4,AC=CD=1可得出AE的长,根据锐角三角函数的定义即可得出结论;
(3)根据(2)中AE的长可得出AD的长,△ABD为圆O过直径的内接三角形,再根据勾股定理即可得出BD的长.
 |
| AC |
 |
| CD |
(2)连接AD,OD,AD和CO相交于E,根据AC=CD,AO=DO可知四边形ACDO的对角线AD和CO互相垂直,由勾股定理可知CE2=AC2-AE2,EO2=AO2-AE2,CE+EO=CO=2,根据AB=4,AC=CD=1可得出AE的长,根据锐角三角函数的定义即可得出结论;
(3)根据(2)中AE的长可得出AD的长,△ABD为圆O过直径的内接三角形,再根据勾股定理即可得出BD的长.
解答: 解:(1)∵AC=CD=1,
解:(1)∵AC=CD=1,
∴
=
,
∴∠AOC=∠ABD,
∴OC∥BD;
(2)连接AD,OD,AD和CO相交于E
∵AC=CD,AO=DO,
∴四边形ACDO的对角线AD和CO互相垂直
∴CE2=AC2-AE2,EO2=AO2-AE2,CE+EO=CO=2,
∵AB=4,AC=CD=1,
∴AE=
∴sinα=
=
=
;
(3)∵由(2)知,AE=
,
∴AD=2AE=
,
∵AB是⊙O的直径,
∴△ABD是直角三角形,
∴BD2=AB2-AD2,即BD2=42-(
)2,
∴BD=
.
 解:(1)∵AC=CD=1,
解:(1)∵AC=CD=1,∴
 |
| AC |
 |
| CD |
∴∠AOC=∠ABD,
∴OC∥BD;
(2)连接AD,OD,AD和CO相交于E
∵AC=CD,AO=DO,
∴四边形ACDO的对角线AD和CO互相垂直
∴CE2=AC2-AE2,EO2=AO2-AE2,CE+EO=CO=2,
∵AB=4,AC=CD=1,
∴AE=
| ||
| 2 |
∴sinα=
| AE |
| OA |
| ||||
| 2 |
| ||
| 4 |
(3)∵由(2)知,AE=
| ||
| 2 |
∴AD=2AE=
| 15 |
∵AB是⊙O的直径,
∴△ABD是直角三角形,
∴BD2=AB2-AD2,即BD2=42-(
| 15 |
∴BD=
| 7 |
| 2 |
点评:本题考查的是垂径定理与勾股定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
相关题目
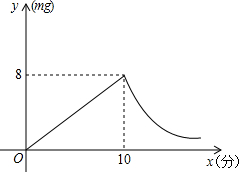 为预防感冒,小王家在家中燃烧艾草,已知艾草燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧停止后,y与x成反比例(如图所示).据图象上信息解答下列问题:
为预防感冒,小王家在家中燃烧艾草,已知艾草燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧停止后,y与x成反比例(如图所示).据图象上信息解答下列问题: 如图所示,有一电路AB是由如图所示的开关控制,闭合a,b,c,d四个开关中的任意两个开关.
如图所示,有一电路AB是由如图所示的开关控制,闭合a,b,c,d四个开关中的任意两个开关. 如图,已知BC=AD,若根据“SSS”证明△ABC≌△BAD,需要添加一个条件,那么这个条件是:
如图,已知BC=AD,若根据“SSS”证明△ABC≌△BAD,需要添加一个条件,那么这个条件是: