题目内容
若分式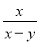 有意义,则x与y的关系是_____.
有意义,则x与y的关系是_____.
 x≠y
【解析】当分母x-y≠0,即x≠y时,分式有意义.故答案是:x≠y.
x≠y
【解析】当分母x-y≠0,即x≠y时,分式有意义.故答案是:x≠y.
练习册系列答案
相关题目
把多项式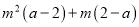 分解因式正确的是 ( )
分解因式正确的是 ( )
A.  B.
B. 
C.  D.
D. 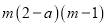
 B
【解析】根据因式分解法—提公因式,可由a-2与2-a互为相反数,先变形,再提公因式a-2可得: = = .
故选:B.
B
【解析】根据因式分解法—提公因式,可由a-2与2-a互为相反数,先变形,再提公因式a-2可得: = = .
故选:B. 如图,MN与PQ相交于点O,MO=OP,QO=ON,∠M=65°,∠Q=30°,则∠P=____,∠N=___.
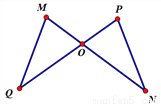
 65° 30°
【解析】∵MO=OP,QO=ON(已知),
∠MO Q=∠PO N(对顶角相等)
∴△MOQ≌△PON(SAS)
∴∠P=∠M=65°,
∠N=∠Q=30°
故答案为:65°;30°
65° 30°
【解析】∵MO=OP,QO=ON(已知),
∠MO Q=∠PO N(对顶角相等)
∴△MOQ≌△PON(SAS)
∴∠P=∠M=65°,
∠N=∠Q=30°
故答案为:65°;30° 若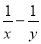 =3 ,求
=3 ,求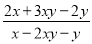 的值.
的值.
 【解析】分析:由已知可知x-y=-3xy,然后代入所求的式子,进行约分就可求出结果.
本题解析:
∵ =3,∴y-x=3xy, ∴x-y=-3xy,
∴ =.
【解析】分析:由已知可知x-y=-3xy,然后代入所求的式子,进行约分就可求出结果.
本题解析:
∵ =3,∴y-x=3xy, ∴x-y=-3xy,
∴ =. 填空:
(1)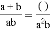 ; (2)
; (2)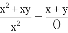 ;
;
(3)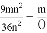 ; (4)
; (4)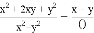 .
.
 ⑴,⑵x,⑶4n,⑷x-y.
【解析】(1)= ,
(2)= ,
(3)=,
(4)=.
故答案为:⑴a²+ab,⑵x,⑶4n,⑷x-y.
⑴,⑵x,⑶4n,⑷x-y.
【解析】(1)= ,
(2)= ,
(3)=,
(4)=.
故答案为:⑴a²+ab,⑵x,⑶4n,⑷x-y. 若代数式 的值为零,则x的值为( )
的值为零,则x的值为( )
A. 2或-1 B. -1 C. ±1 D. 2
 D
【解析】根据题意得:(x-2)(x+1)=0,且 ,
计算得出:x=2,
所以D选项是正确的.
D
【解析】根据题意得:(x-2)(x+1)=0,且 ,
计算得出:x=2,
所以D选项是正确的. 根据不等式的基本性质,可将“mx<2”化为“x>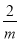 ”,则m的取值范围是_____.
”,则m的取值范围是_____.
 m<0
【解析】因为mx<2化为x>,
根据不等式的基本性质3得:m<0,
故答案为:m<0.
m<0
【解析】因为mx<2化为x>,
根据不等式的基本性质3得:m<0,
故答案为:m<0. 设四边形的内角和等于a,五边形的外角和等于b,则a与b的关系是( )
A. a>b B. a=b C. a<b D. b=a+180°
 B
【解析】∵四边形的内角和等于a,
∴a=(4﹣2)•180°=360°.
∵五边形的外角和等于b,
∴b=360°,
∴a=b.
故选B.
B
【解析】∵四边形的内角和等于a,
∴a=(4﹣2)•180°=360°.
∵五边形的外角和等于b,
∴b=360°,
∴a=b.
故选B. 用不等号连接下列各对数:(1)- _______-
_______-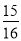 ,(2)
,(2) 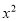 +1 _______0 .
+1 _______0 .
 > >
【解析】(1)∵, ,∴,
故答案为:>;
(2)∵x2≥0,∴x2+1>0,
故答案为:>.
> >
【解析】(1)∵, ,∴,
故答案为:>;
(2)∵x2≥0,∴x2+1>0,
故答案为:>. 
