题目内容
19. 如图,正方形ABCD的边长为4,延长CB至点M,使BM=2,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为$\frac{6\sqrt{10}}{5}$.
如图,正方形ABCD的边长为4,延长CB至点M,使BM=2,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为$\frac{6\sqrt{10}}{5}$.
分析 由条件可证得△ABN∽△BNM∽△ABM,且可求得线段AM的长度,利用对应线段的比相等可求得AN和MN,进一步可得到$\frac{AO}{AM}=\frac{AN}{AC}$,且∠CAM=∠NAO,可证得△AON∽△AMC,利用相似三角形的性质可求得ON.
解答 解:∵AB=4,BM=2,
∴AM=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∵∠ABM=90°,BN⊥AM,
∴△ABN∽△BNM∽△AMB,
∴AB2=AN×AM,BM2=MN×AM,
∴AN=$\frac{8\sqrt{5}}{5}$,MN=$\frac{2\sqrt{5}}{5}$,
∵AB=4,CD=4,
∴AC=4$\sqrt{2}$,
∴AO=2$\sqrt{2}$,
∵$\frac{AO}{AM}=\frac{AN}{AC}$=$\frac{\sqrt{10}}{5}$,且∠CAM=∠NAO
∴△AON∽△AMC,
∴$\frac{ON}{MC}$=$\frac{AO}{AM}$,即$\frac{ON}{6}$=$\frac{2\sqrt{2}}{2\sqrt{5}}$,
∴ON=$\frac{6\sqrt{10}}{5}$.
故答案为:$\frac{6\sqrt{10}}{5}$.
点评 本题考查了正方形性质、勾股定理、相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
16.若点P的坐标是(x,y),且满足x2+$\sqrt{y}$=0,则点P在( )
| A. | x轴的负半轴上 | B. | 第二象限 | C. | y轴的正半轴上 | D. | 坐标原点 |
11. 在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )
在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )
 在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )
在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )| A. | 8056 | B. | 8050 | C. | 8054 | D. | 8052 |
8. 如图,已知三条直线a、b、c,a∥b,c与a、b交于A、C,点B在b上,∠1=65°,AB=BC,则∠2的度数是( )
如图,已知三条直线a、b、c,a∥b,c与a、b交于A、C,点B在b上,∠1=65°,AB=BC,则∠2的度数是( )
 如图,已知三条直线a、b、c,a∥b,c与a、b交于A、C,点B在b上,∠1=65°,AB=BC,则∠2的度数是( )
如图,已知三条直线a、b、c,a∥b,c与a、b交于A、C,点B在b上,∠1=65°,AB=BC,则∠2的度数是( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |

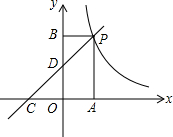 如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,S△PBD=2,OA=OC.求:
如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,S△PBD=2,OA=OC.求: