题目内容
11．
在直线y=-x+4032的图象上有点P1、P2、P3…、P2014，点P1的横坐标为2，且后面每个点的横坐标与它前面相邻点的横坐标的差都是2，过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段，构成若干个长方形，如图所示，将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014，则S1+S2+S3…+S2014=（ ）| A． | 8056 | B． | 8050 | C． | 8054 | D． | 8052 |
分析 根据一次函数图象上点的坐标特征结合xn+1-xn=2，可得出yn+1-yn=-2，结合矩形的面积公式即可得出Sn=4，由此即可得出结论．
解答 解：∵xn+1-xn=2，且一次函数解析式为y=-x+4032，
∴yn+1-yn=-（xn+1-xn）=-2，（1≤n≤2015）
∴Sn=|xn+1-xn|•|yn+1-yn|=2×2=4．
∴S1+S2+S3…+S2014=4×2014=8056．
故选A．
点评 本题考查了一次函数图象上点的坐标特征，解题的关键是找出Sn=4．本题属于基础题，难度不大，解决该题型题目时，根据一次函数图象上点的坐标特征找出矩形的长和宽，求出矩形的面积公式是关键．
练习册系列答案
相关题目
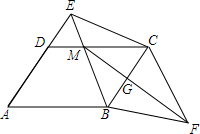如图所示，点M是平行四边形ABCD的边CD上一点，且DM：MC=1：2，四边形EBFC为平行四边形，FM与BC交于点G．若三角形FCG的面积与三角形MED的面积之差为13cm2，平行四边形ABCD的面积是60cm2．
如图，正方形ABCD的边长为4，延长CB至点M，使BM=2，过点B作BN⊥AM，垂足为N，O是对角线AC，BD的交点，连接ON，则ON的长为$\frac{6\sqrt{10}}{5}$．
如图，在矩形ABCD中，点F在边BC上，且AF=AD，过点D作DE⊥AF，垂足为点E．以D为圆心，DE为半径作圆弧交AD于点G，若BF=FC=1，则$\widehat{EG}$的长为$\frac{\sqrt{3}π}{6}$．
20．
某小学三年级到六年级的全体学生参加“礼仪”知识测试，试题共有10题，每题10分．从中随机抽取了部分学生的成绩进行统计，发现抽测的学生每人至少答对了6题，现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”．
成绩情况统计表
根据图表中提供的信息，回答下列问题：
（1）测试学生中，成绩为80分的学生人数有36名；众数是90分；中位数是90分；
（2）若该小学三年级到六年级共有1800名学生，则可估计出成绩为70分的学生人数约有270名．
某小学三年级到六年级的全体学生参加“礼仪”知识测试，试题共有10题，每题10分．从中随机抽取了部分学生的成绩进行统计，发现抽测的学生每人至少答对了6题，现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”．成绩情况统计表
| 成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
| 人数 | 21 | 40 | 36 | 18 | 5 |
| 频率 | 0.175 | 0.333 | 0.3 | 0.15 | 0.04 |
（1）测试学生中，成绩为80分的学生人数有36名；众数是90分；中位数是90分；
（2）若该小学三年级到六年级共有1800名学生，则可估计出成绩为70分的学生人数约有270名．
