题目内容
7.已知线段DE别交△ABC的边AB、AC于D、E,且$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$=$\frac{5}{3}$,△ABC的周长是100cm,面积是75cm2,求△ADE的周长和面积.分析 根据已知比例式推出△ADE∽△ABC,$\frac{AB+AC+BC}{AD+AE+DE}$=$\frac{5}{3}$,再根据相似三角形的性质推出即可.
解答 解:如图: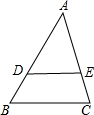
∵$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$=$\frac{5}{3}$,
∴△ADE∽△ABC,$\frac{AB+AC+BC}{AD+AE+DE}$=$\frac{5}{3}$,
∴$\frac{{S}_{△ABC}}{{S}_{△ADE}}$=($\frac{5}{3}$)2=$\frac{25}{9}$,
∵△ABC的周长是100cm,面积是75cm2,
∴△ADE的周长为60cm,面积是27cm2.
点评 本题考查了相似三角形的判定和性质的应用,能熟记相似三角形的性质是解此题的关键,注意:相似三角形的周长之比等于相似比,相似三角形的面积之比等于相似比的平方.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
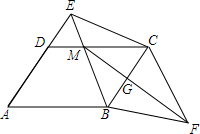 如图所示,点M是平行四边形ABCD的边CD上一点,且DM:MC=1:2,四边形EBFC为平行四边形,FM与BC交于点G.若三角形FCG的面积与三角形MED的面积之差为13cm2,平行四边形ABCD的面积是60cm2.
如图所示,点M是平行四边形ABCD的边CD上一点,且DM:MC=1:2,四边形EBFC为平行四边形,FM与BC交于点G.若三角形FCG的面积与三角形MED的面积之差为13cm2,平行四边形ABCD的面积是60cm2.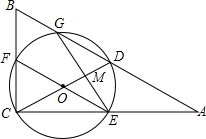 如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O分别交边AB、BC,AC于点G,F,E,GE交CD于点M,ME=4$\sqrt{6}$,MD:CO=2:5.
如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O分别交边AB、BC,AC于点G,F,E,GE交CD于点M,ME=4$\sqrt{6}$,MD:CO=2:5. 如图,正方形ABCD的边长为4,延长CB至点M,使BM=2,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为$\frac{6\sqrt{10}}{5}$.
如图,正方形ABCD的边长为4,延长CB至点M,使BM=2,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为$\frac{6\sqrt{10}}{5}$. 如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.以D为圆心,DE为半径作圆弧交AD于点G,若BF=FC=1,则$\widehat{EG}$的长为$\frac{\sqrt{3}π}{6}$.
如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.以D为圆心,DE为半径作圆弧交AD于点G,若BF=FC=1,则$\widehat{EG}$的长为$\frac{\sqrt{3}π}{6}$. 如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.
如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.