题目内容
定义：n！=1×2×3×…×（n-1）×n，例如：4！=1×2×3×4，化简：
+
+
+…+
= ．
| 1 |
| 2！ |
| 2 |
| 3！ |
| 3 |
| 4！ |
| n |
| (n+1)! |
考点：有理数的混合运算
专题：新定义
分析：原式利用题中的新定义变形，找出规律，以此类推得到结果即可．
解答：解：原式=
+
+
+…+
=1-
+
+
+…+
=1-
+
+…+
=1-
+
+…+
=1-
+
+
+…+
…
=1-
+
=1-
+
=1-
．
故答案为：1-
．
| 2！-1 |
| 2！ |
| 2 |
| 3！ |
| 3 |
| 4！ |
| n |
| (n+1)！ |
=1-
| 1 |
| 2！ |
| 2 |
| 3！ |
| 3 |
| 4！ |
| n |
| (n+1)！ |
=1-
| 1 |
| 3！ |
| 3 |
| 4！ |
| n |
| (n+1)！ |
=1-
| 4 |
| 4！ |
| 3 |
| 4！ |
| n |
| (n+1)！ |
=1-
| 1 |
| 4！ |
| 2 |
| 3！ |
| 3 |
| 4！ |
| n |
| (n+1)！ |
…
=1-
| 1 |
| n！ |
| n |
| (n+1)！ |
=1-
| n+1 |
| (n+1)！ |
| n |
| (n+1)！ |
=1-
| 1 |
| (n+1)！ |
故答案为：1-
| 1 |
| (n+1)！ |
点评：此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
小雨的爸爸从市场买回来四个大西瓜，爸爸为了考一考小雨，让小雨把四个大西瓜依次边上①，②，③，④号后，按质量由小到大的顺序排列出来（不准用称），小雨用一个简易天平操作，操作如下：（操作过程中，天平自身损坏忽略不计）
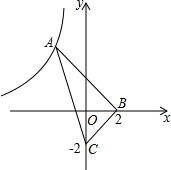如图，△ABC的内心在x轴上，点B的坐标是（2，0），点C的坐标是（0，-2），点A的坐标是（-3，b），反比例函数y=
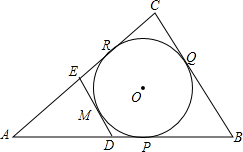如图，⊙O内切于△ABC，P，Q，R为切点，⊙O的切线DE∥BC，M为切点，D，E分别在AB，AC上，已知BC=2，△ABC的周长为8，⊙O的半径为1，则S△ADE=
如图是一个几何体的三视图，其中主视图、左视图都是腰为13cm，底为10cm的等腰三角形，求这个几何体的体积．