Question

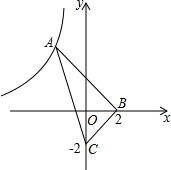如图，△ABC的内心在x轴上，点B的坐标是（2，0），点C的坐标是（0，-2），点A的坐标是（-3，b），反比例函数y=

k

x

（x＜0）的图象经过点A，
则k=

 

．

Answer 1

考点：三角形的内切圆与内心,反比例函数图象上点的坐标特征

专题：计算题

分析：根据内心的性质得OB平分∠ABC，再由点B的坐标是（2，0），点C的坐标是（0，-2）得到△OBC为等腰直角三角形，则∠OBC=45°，所以∠ABC=90°，利用勾股定理有AB²+BC²=AC²，根据两点间的距离公式得到（-3-2）²+b²+2²+2²=（-3）²+（b+2）²，解得b=5，然后根据反比例函数图象上点的坐标特征求k的值．

解答：解：∵△ABC的内心在x轴上，
∴OB平分∠ABC，
∵点B的坐标是（2，0），点C的坐标是（0，-2），
∴OB=OC，
∴△OBC为等腰直角三角形，
∴∠OBC=45°，
∴∠ABC=90°，
∴AB²+BC²=AC²，
∴（-3-2）²+b²+2²+2²=（-3）²+（b+2）²，解得b=5，
∴A点坐标为（-3，5），
∴k=-3×5=-15．
故答案为-15．

点评：本题考查了三角形的内切圆与内心：与三角形各边都相切的圆叫三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．三角形的内心就是三角形三个内角角平分线的交点．也考查了反比例函数图象上点的坐标特征和两点间的距离公式．