题目内容
8.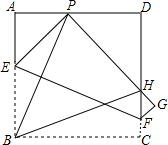 如图,现有一张边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,联结BP、BH,当AP=1时,则PH=3.4,EF=$\sqrt{17}$.
如图,现有一张边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,联结BP、BH,当AP=1时,则PH=3.4,EF=$\sqrt{17}$.
分析 根据翻折变换的性质得出∠PBC=∠BPH,进而利用平行线的性质得出∠APB=∠PBC,根据全等三角形的性质得到AP+HC=PH,设QH=HC=x,则DH=4-x.根据勾股定理列方程求解即可.
解答 解:∵PE=BE,
∴∠EPB=∠EBP,
又∵∠EPH=∠EBC=90°,
∴∠EPH-∠EPB=∠EBC-∠EBP.
即∠BPH=∠PBC.
又∵四边形ABCD为正方形,
∴AD∥BC,
∴∠APB=∠PBC.
∴∠APB=∠BPH,
过B作BQ⊥PH,垂足为Q,
在△ABP与△QBP中,$\left\{\begin{array}{l}{∠A=∠BQP=90°}\\{∠APB=∠BPH}\\{BP=BP}\end{array}\right.$,
∴△ABP≌△QBP(AAS),
∴AP=QP,BA=BQ.
又∵AB=BC,
∴BC=BQ.
又∵∠C=∠BQH=90°,
∴△BCH和△BQH是直角三角形,
在Rt△BCH与Rt△BQH中,$\left\{\begin{array}{l}{BC=BQ}\\{BH=BH}\end{array}\right.$,
∴Rt△BCH≌Rt△BQH(HL),
∴CH=QH,
∴AP+HC=PH,
∵AP=PQ=1,
∴PD=3,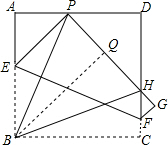
设QH=HC=x,则DH=4-x,
在Rt△PDH中,PD2+DH2=PH2,
即32+(4-x)2=(x+1)2,
解得x=2.4,
∴PH=3.4,
设CF=y,HF=2.4-y,
∴(2.4-y)2=y2+0.62,
∴y=$\frac{9}{8}$,
∵BE=PE,PE2=AE2+AP2,∴BE2=(4-BE)2+1,
∴BE=$\frac{17}{8}$,
∴EF2=42+($\frac{17}{8}$-$\frac{9}{8}$)2=17,
∴EF=$\sqrt{17}$.
故答案为:3.4,$\sqrt{17}$.
点评 此题主要考查了翻折变换的性质以及全等三角形的判定与性质和勾股定理等知识,熟练利用全等三角形的判定得出对应相等关系是解题关键.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案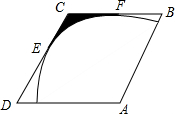 如图,菱形ABCD的边长为2,∠A=120°,以点A为圆心的圆弧与菱形ABCD的DC,BC两边相切,切点分别为点E、F,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π.
如图,菱形ABCD的边长为2,∠A=120°,以点A为圆心的圆弧与菱形ABCD的DC,BC两边相切,切点分别为点E、F,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π. 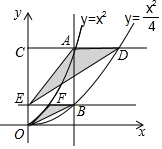 如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=$\frac{{x}^{2}}{4}$(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为( )
如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=$\frac{{x}^{2}}{4}$(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为( )| A. | $\frac{\sqrt{2}}{6}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
 有这样一个问题:探究方程x3-x-2=0的实数根的个数.
有这样一个问题:探究方程x3-x-2=0的实数根的个数. 将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,求∠1+∠2的值.
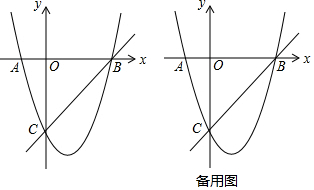
将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,求∠1+∠2的值. 在平面直角坐标系xOy中,已知直线y=ax+b与x轴,y轴交于A,B两点,点C的坐标为(a,b).
在平面直角坐标系xOy中,已知直线y=ax+b与x轴,y轴交于A,B两点,点C的坐标为(a,b).