题目内容
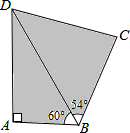
9．
如图，在四边形ABCD中，已知∠B=60°，∠C=2∠B，由这些条件你能判断平行的两条直线是AB∥CD．
分析 先根据题意得出∠C的度数，再由平行线的判定定理即可得出结论．
解答 解：∵在四边形ABCD中，∠B=60°，∠C=2∠B，
∴∠C=120°，
∴∠B+∠C=180°，
∴AB∥CD．
故答案为：AB∥CD．
点评 本题考查的是平行线的判定，用到的知识点为：同旁内角互补，两直线平行．
练习册系列答案
相关题目
如图，四边形ABCD是一片水田，某村民小组需计算其面积，测得如下数据：
如图，⊙P经过点A（0，$\sqrt{3}$）、O（0，0）、B（1，0），点C在第一象限的$\widehat{AB}$上，则∠BCO的度数为30°．
17．如果一个单项式除以-3ab的商为$\frac{1}{4}$ac，则这个单项式是（ ）
| A． | $\frac{3}{4}{a}^{2}bc$ | B． | $-\frac{3}{4}{a}^{2}bc$ | C． | $\frac{1}{4}{a}^{2}b$ | D． | $\frac{9}{4}ab$ |
4．
如图，在平面直角坐标系中，直线y=$\frac{3}{4}$x+6交x轴于点A，交y轴于点B，D1是线段AB的中点，过D1作D1E1⊥x轴于E1，连接BE1交OD1于D2；过D2作D2E2⊥x轴于E2，连接BE2交OD1于D3；过D3作D3E3⊥x轴于E3，…，如此继续，可以依次得到点D4，D5，…，Dn，分别记△BD1E1，△BD2E2，△BD3E3，…，△BDnEn的面积为S1，S2，S3，…Sn．则Sn为（ ）
如图，在平面直角坐标系中，直线y=$\frac{3}{4}$x+6交x轴于点A，交y轴于点B，D1是线段AB的中点，过D1作D1E1⊥x轴于E1，连接BE1交OD1于D2；过D2作D2E2⊥x轴于E2，连接BE2交OD1于D3；过D3作D3E3⊥x轴于E3，…，如此继续，可以依次得到点D4，D5，…，Dn，分别记△BD1E1，△BD2E2，△BD3E3，…，△BDnEn的面积为S1，S2，S3，…Sn．则Sn为（ ）| A． | $\frac{24}{（n+1）^{2}}$ | B． | $\frac{12}{（n+1）^{2}}$ | C． | $\frac{24}{{n}^{2}}$ | D． | $\frac{12}{{n}^{2}}$ |
14．某商店需要购进A、B两种商品共160件，其进价和售价如表：
（1）当A、B两种商品分别购进多少件时，商店计划售完这批商品后能获利1100元；
（2）若商店计划购进A种商品不少于66件，且销售完这批商品后获利多于1260元，请你帮该商店老板预算有几种购货方案？获利最大是多少元？
| A | B | |
| 进价（元/件） | 15 | 35 |
| 售价（元/件） | 20 | 45 |
（2）若商店计划购进A种商品不少于66件，且销售完这批商品后获利多于1260元，请你帮该商店老板预算有几种购货方案？获利最大是多少元？
1．电影《刘三姐》中，秀才和刘三姐对歌的场面十分精彩．罗秀才唱道：“三百条狗交给你，一少三多四下分，
不要双数要单数，看你怎样分得均？”刘三姐示意舟妹来答，舟妹唱道：“九十九条打猎去，九十九条看羊来，九十九条守门口，剩下三条财主请来当奴才．”若用数学方法解决罗秀才提出的问题，设“一少”的狗有x条，“三多”的狗有y条，则解此问题所列关系式正确的是（ ）
不要双数要单数，看你怎样分得均？”刘三姐示意舟妹来答，舟妹唱道：“九十九条打猎去，九十九条看羊来，九十九条守门口，剩下三条财主请来当奴才．”若用数学方法解决罗秀才提出的问题，设“一少”的狗有x条，“三多”的狗有y条，则解此问题所列关系式正确的是（ ）
| A． | $\left\{\begin{array}{l}x+3y=300\\ 0＜x＜y＜300\end{array}\right.$ | |
| B． | $\left\{\begin{array}{l}{x+3y=300}\\{0＜x＜y＜300}\\{x、y是奇数}\end{array}\right.$ | |
| C． | $\left\{\begin{array}{l}{x+3y=300}\\{0＜3x=y＜300}\\{x、y是奇数}\end{array}\right.$ | |
| D． | $\left\{\begin{array}{l}{x+3y=300}\\{0＜x＜300，0＜y＜300}\\{x、y是奇数}\end{array}\right.$ |