题目内容
1.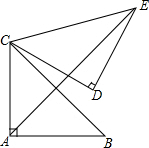 如图,在△ABC中,∠BAC=90°,AB=AC=2,将△CAB绕着点C逆时针旋转60°,得到△CDE,连接AE,则AE的长是$\sqrt{2}$+$\sqrt{6}$.
如图,在△ABC中,∠BAC=90°,AB=AC=2,将△CAB绕着点C逆时针旋转60°,得到△CDE,连接AE,则AE的长是$\sqrt{2}$+$\sqrt{6}$.
分析 如图,连接AM,由题意得:CA=CM,∠ACM=60°,得到△ACM为等边三角形,根据AB=BC,CM=AM,得出BM垂直平分AC,于是求出BO=$\frac{1}{2}$AC=$\sqrt{2}$,OM=CM•sin60°=$\sqrt{6}$,最终得到BM=BO+OM.
解答 解:如图,连接AM,
由题意得:CA=CM,∠ACM=60°,
∴△ACM为等边三角形,
∴AM=CM,∠MAC=∠MCA=∠AMC=60°;
∵∠ABC=90°,AB=BC=2,
∴AC=CM=2$\sqrt{2}$,
∵AB=BC,CM=AM,
∴BM垂直平分AC,
∴BO=$\frac{1}{2}$AC=$\sqrt{2}$,OM=CM•sin60°=$\sqrt{6}$,
∴BM=BO+OM=$\sqrt{2}$+$\sqrt{6}$,
故答案为:$\sqrt{2}$+$\sqrt{6}$.
点评 本题考查了图形的变换-旋转,等腰直角三角形的性质,等边三角形的判定和性质,线段的垂直平分线的性质,准确把握旋转的性质是解题的关键.

练习册系列答案
相关题目
6.某校九年级两个班,各选派10名学生参加学校举行的“数学奥林匹克”大赛预赛.各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
(1)直接写出表中a、b的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
| 班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
| 九(1)班 | 100 | 94 | b | 93 | 12 |
| 九(2)班 | 99 | a | 95.5 | 93 | 8.4 |
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.
13. 已知一次函数y=kx+b的图象如图所示,则关于x的不等式k(x-4)-2b≥0的解集为( )
已知一次函数y=kx+b的图象如图所示,则关于x的不等式k(x-4)-2b≥0的解集为( )
 已知一次函数y=kx+b的图象如图所示,则关于x的不等式k(x-4)-2b≥0的解集为( )
已知一次函数y=kx+b的图象如图所示,则关于x的不等式k(x-4)-2b≥0的解集为( )| A. | x≥-2 | B. | x≤-2 | C. | x≤3 | D. | x≥3 |
 已知反比例函数y=$\frac{k}{x}$的图象如图所示,则二次函数y=-kx2-2x+$\frac{{k}^{2}}{4}$的图象大致为( )
已知反比例函数y=$\frac{k}{x}$的图象如图所示,则二次函数y=-kx2-2x+$\frac{{k}^{2}}{4}$的图象大致为( )



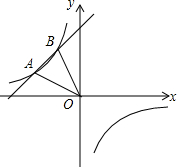 如图,一次函数的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-4,a)、B两点,点B的横坐标比点A的横坐标大2,且S△AOB=6.
如图,一次函数的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-4,a)、B两点,点B的横坐标比点A的横坐标大2,且S△AOB=6. 如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,经过A、D两点的圆的圆心O恰好落在AB上,⊙O分别与AB、AC相交于点E、F.
如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,经过A、D两点的圆的圆心O恰好落在AB上,⊙O分别与AB、AC相交于点E、F.