题目内容
10. 如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,经过A、D两点的圆的圆心O恰好落在AB上,⊙O分别与AB、AC相交于点E、F.
如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,经过A、D两点的圆的圆心O恰好落在AB上,⊙O分别与AB、AC相交于点E、F.(1)判断直线BC与⊙O的位置关系并证明;
(2)若⊙O的半径为2,AC=3,求BD的长度.
分析 (1)连接OD,证明OD∥AC,即可证得∠ODB=90°,从而证得BC是圆的切线;
(2)由OD∥AC,证得△BDO∽△BCA,根据相似三角形的性质得出$\frac{BE+2}{BE+4}$=$\frac{2}{3}$,解得BE=2,然后根据勾股定理即可求得BD的长度.
解答 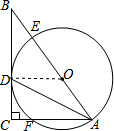 解:(1)BC与⊙O相切.
解:(1)BC与⊙O相切.
证明:连接OD.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
又∵OD=OA,
∴∠OAD=∠ODA.
∴∠CAD=∠ODA.
∴OD∥AC.
∴∠ODB=∠C=90°,即OD⊥BC.
又∵BC过半径OD的外端点D,
∴BC与⊙O相切.
(2)由(1)知OD∥AC.
∴△BDO∽△BCA.
∴$\frac{BO}{BA}$=$\frac{DO}{CA}$.
∵⊙O的半径为2,
∴DO=OE=2,AE=4.
∴$\frac{BE+2}{BE+4}$=$\frac{2}{3}$.
∴BE=2.
∴BO=4,
∴在Rt△BDO中,BD=$\sqrt{B{O}^{2}-O{D}^{2}}$=2$\sqrt{3}$.
点评 本题考查了切线的判定,以及相似三角形的判定和性质、勾股定理的应用,要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
18.计算:$\frac{{a}^{2}-1}{{a}^{2}+2a+1}$÷$\frac{a-1}{a}$,其结果正确的是( )
| A. | $\frac{1}{2}$ | B. | $\frac{a}{a+1}$ | C. | $\frac{a+1}{a}$ | D. | $\frac{a+1}{a+2}$ |
2. 如图,已知∠1=50°,如果CD∥BE,那么∠B的度数是( )
如图,已知∠1=50°,如果CD∥BE,那么∠B的度数是( )
 如图,已知∠1=50°,如果CD∥BE,那么∠B的度数是( )
如图,已知∠1=50°,如果CD∥BE,那么∠B的度数是( )| A. | 50° | B. | 100° | C. | 120° | D. | 130° |
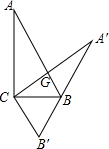 如图,在Rt△ABC中,∠C=90°,BC=5,tanB=2,把△ABC绕点C旋转得到△A′B′C,此时AB的对应边A′B′恰好经过点B,又A′C交AB于点G,则线段CG的长是$\frac{50}{11}$.
如图,在Rt△ABC中,∠C=90°,BC=5,tanB=2,把△ABC绕点C旋转得到△A′B′C,此时AB的对应边A′B′恰好经过点B,又A′C交AB于点G,则线段CG的长是$\frac{50}{11}$.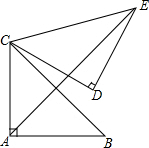 如图,在△ABC中,∠BAC=90°,AB=AC=2,将△CAB绕着点C逆时针旋转60°,得到△CDE,连接AE,则AE的长是$\sqrt{2}$+$\sqrt{6}$.
如图,在△ABC中,∠BAC=90°,AB=AC=2,将△CAB绕着点C逆时针旋转60°,得到△CDE,连接AE,则AE的长是$\sqrt{2}$+$\sqrt{6}$. 如图,已知BD∥CA,∠A=40°,∠DBE=65°,则∠ABC的大小是75°.
如图,已知BD∥CA,∠A=40°,∠DBE=65°,则∠ABC的大小是75°.