题目内容
11.已知m是关于x的一元二次方程x2+nx+m=0的一个根,且m≠0,则m+n的值是-1.分析 根据一元二次方程的解的定义把x=m代入x2+nx+m=0得到m2+mn+m=0,继而可得m+n的值.
解答 解:∵m是关于x的一元二次方程x2+nx+m=0的一个根,
∴m2+mn+m=0,即m(m+n+1)=0,
∵m≠0,
∴m+n+1=0,即m+n=-1,
故答案为:-1.
点评 本题考查了一元二次方程的解(根):能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.

练习册系列答案
相关题目
6.下列命题错误的是( )
| A. | 平行四边形的对角线互相平分 | |
| B. | 对角线互相垂直平分的四边形是菱形 | |
| C. | 矩形的对角线相等 | |
| D. | 对角线相等的四边形是正方形 |
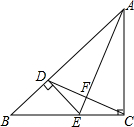 已知,如图,△ABC中,AC=BC,∠C=90°,AE平分∠BAC交BC于E,过E做ED⊥AB于D,连接DC交AE于F,其中BD=1.则在下列结论中:①AE⊥DC;②AB=2+$\sqrt{2}$;③$\frac{AE}{CD}$=2;④AE•CD=2+2$\sqrt{2}$.其中正确的结论是①②④.
已知,如图,△ABC中,AC=BC,∠C=90°,AE平分∠BAC交BC于E,过E做ED⊥AB于D,连接DC交AE于F,其中BD=1.则在下列结论中:①AE⊥DC;②AB=2+$\sqrt{2}$;③$\frac{AE}{CD}$=2;④AE•CD=2+2$\sqrt{2}$.其中正确的结论是①②④. 如图,直线AB与反比例函数y=$\frac{4}{x}$(x>0)的图象交于点A(u,p)和点B(v,q),与x轴交于点C,已知∠ACO=45°,若$\frac{1}{3}$<u<2,求v的取值范围.
如图,直线AB与反比例函数y=$\frac{4}{x}$(x>0)的图象交于点A(u,p)和点B(v,q),与x轴交于点C,已知∠ACO=45°,若$\frac{1}{3}$<u<2,求v的取值范围. 如图,在矩形ABCD中,AB=2,BC=4,M是AD的中点,动点E在线段AB上,连结EM并延长交射线CD于点F,过点M作EF的垂线交BC于点G,连结EG、FG.
如图,在矩形ABCD中,AB=2,BC=4,M是AD的中点,动点E在线段AB上,连结EM并延长交射线CD于点F,过点M作EF的垂线交BC于点G,连结EG、FG.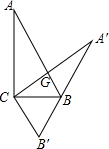 如图,在Rt△ABC中,∠C=90°,BC=5,tanB=2,把△ABC绕点C旋转得到△A′B′C,此时AB的对应边A′B′恰好经过点B,又A′C交AB于点G,则线段CG的长是$\frac{50}{11}$.
如图,在Rt△ABC中,∠C=90°,BC=5,tanB=2,把△ABC绕点C旋转得到△A′B′C,此时AB的对应边A′B′恰好经过点B,又A′C交AB于点G,则线段CG的长是$\frac{50}{11}$.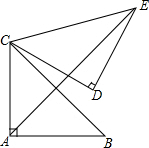 如图,在△ABC中,∠BAC=90°,AB=AC=2,将△CAB绕着点C逆时针旋转60°,得到△CDE,连接AE,则AE的长是$\sqrt{2}$+$\sqrt{6}$.
如图,在△ABC中,∠BAC=90°,AB=AC=2,将△CAB绕着点C逆时针旋转60°,得到△CDE,连接AE,则AE的长是$\sqrt{2}$+$\sqrt{6}$.